题目内容
8.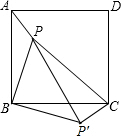 如图,点P是正方形ABCD内的一点,连接AP,BP,CP.将△PAB绕着点B顺时针旋转90°到△P′CB的位置,若AP=2,BP=4,∠APB=135°.求PP′及PC的长.
如图,点P是正方形ABCD内的一点,连接AP,BP,CP.将△PAB绕着点B顺时针旋转90°到△P′CB的位置,若AP=2,BP=4,∠APB=135°.求PP′及PC的长.
分析 根据勾股定理以及旋转性质即可求出PP′,欲求PC只要证明△PP′C是直角三角形,然后利用勾股定理解决.
解答  解:∵△BCP′是由△ABP顺时针旋转90°所得
解:∵△BCP′是由△ABP顺时针旋转90°所得
∴BP′=BP=4,P′C=AP=2,∠PBP′=90°,
∴PP′=$\sqrt{P{B}^{2}+P′{B}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
∵∠BP′C=∠BPA=135°,
∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,
∴PC=$\sqrt{P′{P}^{2}+P′{C}^{2}}$=$\sqrt{(4\sqrt{2})^{2}+{2}^{2}}$=6.
点评 本题考查正方形的性质、旋转的性质、勾股定理等知识,解题的关键是135°角的应用,由135°推出∠PP′C=90°,属于中考常考题型.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
18.下列各组数中,互为相反数的是( )
| A. | 3和-3 | B. | 3和-$\frac{1}{3}$ | C. | -3和$\frac{1}{3}$ | D. | 3和$\frac{1}{3}$ |
16.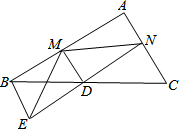 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
(1)求证:BE=CN;
(2)试判断BM+CN与MN的大小关系,并说明理由.
 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.(1)求证:BE=CN;
(2)试判断BM+CN与MN的大小关系,并说明理由.
3.在平面直角坐标系中,抛物线y=x2+2x-3与x轴的交点个数是( )
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
13.2014年2月6日中国民航网报道,马年春节石家庄机场共运送旅客10.2万人次,要反映石家庄2月1日至6日的飞机客流量的变化趋势,宜采用( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 频数分布直方图 |
20.下列方程中,是二元一次方程的为( )
| A. | $x-\frac{1}{x}=3$ | B. | x+xy=-1 | C. | $\frac{x}{3}-\frac{y}{5}=6$ | D. | x2-2x-1=0 |
 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.