题目内容

6．若等腰三角形的两边分别是一元二次方程x2-12x+32=0的两根，则等腰三角形的周长为20．

分析 求出方程的解，根据三角形的三边关系定理得到等腰三角形的三边只能是4，8，8，进一步求出周长即可．

解答 解：∵一元二次方程x2-12x+32=0，
∴解方程得：x1=4，x2=8，
∵等腰三角形的两边分别是一元二次方程x2-12x+32=0的两根，
∴若三角形的腰长为4则4+4=8，构不成三角形，故排除，
∴三角形的腰长为8，底边长为4，
∴三角形的周长=8+8+4=20，
故答案为：20．

点评 本题主要考查对解一元二次方程-因式分解法，三角形的三边关系定理，等腰三角形的性质等知识点的理解和掌握，能求出符合条件的所有情况是解此题的关键．

练习册系列答案
相关题目
1．已知a，b为两个连续的整数，且a$＜\sqrt{23}$＜b，则a+b=9．
17．下列各式能用平方差公式分解因式的有（　　）
①x2+y2；②x2-y2；③-x2-y2；④-x2+y2；⑤-x2+2xy-y2．
A．1个B．2个C．3个D．4个
14．已知a、b、c均是不等于0的有理数，则$\frac{a}{|a|}+\frac{|b|}{b}+\frac{c}{|c|}+\frac{{|{ab}|}}{ab}+\frac{bc}{{|{bc}|}}+\frac{{|{ac}|}}{ac}+\frac{abc}{{|{abc}|}}$的值为7或-1．
1．若方程（a-3）x2+4x+3-|a|=0的一根为0，则a=-3，另一根是$\frac{2}{3}$．
11．①$\frac{1}{x-1}-\frac{3}{x+1}=\frac{x+3}{{{x^2}-1}}$；                        
②$\frac{x}{x-2}-\frac{1}{{{x^2}-4}}=1$．
18．下列各组数中，互为相反数的是（　　）
A．3和-3B．3和-$\frac{1}{3}$C．-3和$\frac{1}{3}$D．3和$\frac{1}{3}$
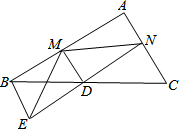15．在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球，这三个小球除颜色外其余都相同，若分别从两个口袋中随机取出一个小球，则取出的两个小球颜色相同的概率是$\frac{1}{3}$．
16．如图，已知D是△ABC中一边BC上的中点，AC∥BE，连接ED并延长ED交AC于点N，作DM⊥EN于点D交AB于点M．
（1）求证：BE=CN；
（2）试判断BM+CN与MN的大小关系，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网