题目内容
7.已知哎平面直角坐标系xOy中,过P(1,1)的直线l与x轴、y轴正半轴交于点A,点B,若三角形AOB的面积等于3,直线l的解析式为y=(-2+$\sqrt{3}$)x+3-$\sqrt{3}$或y=(-2-$\sqrt{3}$)x+3+$\sqrt{3}$.分析 设直线l的解析式为y=kx+b,得出交点A(0,b),B(-$\frac{b}{k}$,0),把P(1,1)代入得出b=1-k,根据三角形面积公式列出关于b、k的方程,进而转化为k的方程,解方程即可求得相似k和b.
解答 解:设直线l的解析式为y=kx+b,
∵过P(1,1),
∴1=k+b,
∴b=1-k,
∵直线l与x轴、y轴正半轴交于点A,点B,若三角形AOB的面积等于3,
∴交点A(0,b),B(-$\frac{b}{k}$,0),
由题意b>0,-$\frac{b}{k}$>0,∴k<0,
∴$\frac{1}{2}$•b•(-$\frac{b}{k}$)=3,
解得b2=-6k,
∴(1-k)2+6k=0,
解得k=-2±$\sqrt{3}$,
∴直线l的解析式为y=(-2+$\sqrt{3}$)x+3-$\sqrt{3}$或y=(-2-$\sqrt{3}$)x+3+$\sqrt{3}$;
故答案为y=(-2+$\sqrt{3}$)x+3-$\sqrt{3}$或y=(-2-$\sqrt{3}$)x+3+$\sqrt{3}$.
点评 本题考查了待定系数法求一次函数的解析式,设出解析式表示出交点坐标以及表示出k与b的关系式是解题的关键.

练习册系列答案
相关题目
18.下列各组数中,互为相反数的是( )
| A. | 3和-3 | B. | 3和-$\frac{1}{3}$ | C. | -3和$\frac{1}{3}$ | D. | 3和$\frac{1}{3}$ |
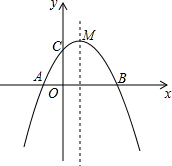 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论:
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论: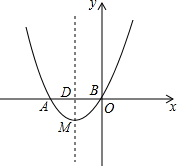 关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn.
关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn. 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.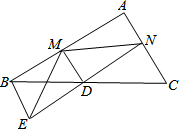 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.