题目内容
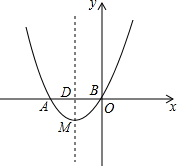
4. 如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.
如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.(1)求抛物线的函数关系式;
(2)设点M(3,m),求使MC+MD的值最小时m的值;
(3)若P是该抛物线上位于直线AB上方的一动点,求△APB面积的最大值.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据轴对称的性质,可得C′点,根据两点之间线段最短,可得M点,根据待定系数法,可得DC′的解析式,根据自变量与函数值的对应关系,可得答案;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PE的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案.
解答 解:(1)将A、B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{-1-b+c=0}\\{-4+2b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
抛物线的解析式为y=-x2+2x+3;
(2)如图1,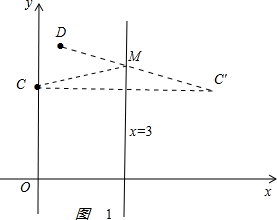 ,
,
作C关于x=3的对称点C′,C′点的坐标(6,3).
连接C′D,C′D交x=3于M点,
设C′D的解析式为y=kx+b,将C′,D的坐标代入函数解析式,得
$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=\frac{21}{5}}\end{array}\right.$,
C′D的解析式为y=-$\frac{1}{5}$x+$\frac{21}{5}$,
当x=3时,y=-$\frac{1}{5}$×3+$\frac{21}{5}$=$\frac{18}{5}$,
即M点坐标(-$\frac{1}{5}$,$\frac{18}{5}$);
(3)如图2,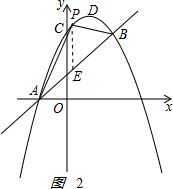 ,
,
AB的解析式为y=kx+b,将A、B点的坐标代入函数解析式,得
$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
AB的解析式为y=x+1,
设E点坐标为E(m,m+1),P(m,-m2+2m+3),
PE═-m2+2m+3-(m+1)=-(m-$\frac{1}{2}$)2+$\frac{9}{4}$,
S△APB=$\frac{1}{2}$PE(xB-xA)
=$\frac{1}{2}$×[-(m-$\frac{1}{2}$)2+$\frac{9}{4}$]×[3-(-1)]
=2×[-(m-$\frac{1}{2}$)2+$\frac{9}{4}$]
当m=$\frac{1}{2}$时,S最大=2×$\frac{9}{4}$=$\frac{9}{2}$.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用轴对称的性质得出C′点是解题关键;利用三角形的面积得出二次函数得出二次函数的性质是解题关键.

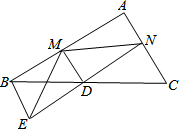 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.(1)求证:BE=CN;
(2)试判断BM+CN与MN的大小关系,并说明理由.
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 频数分布直方图 |
 关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn.
关于x的二次函数y=x2+(2n+1)x+n,它的图象为抛物线Cn,顶点为Mn. 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80. 如图,△ABD≌△BAC,若AD=BC,则∠D的对应角为∠C.
如图,△ABD≌△BAC,若AD=BC,则∠D的对应角为∠C.