题目内容
2.阅读理解:计算$\sqrt{5}$+$\sqrt{6}$+2$\sqrt{5}$-3$\sqrt{6}$时我们可以将式子中的$\sqrt{5}$、$\sqrt{6}$分别看成两个相同的字母a、b;则原式可看成a+b+2a-3b,我们用类比合并同类项的方法可将上面的式子化简.解:$\sqrt{5}$+$\sqrt{6}$+2$\sqrt{5}$-3$\sqrt{6}$
=(1+2)$\sqrt{5}$+(1-3)$\sqrt{6}$
=3$\sqrt{5}$-2$\sqrt{6}$
类比以上解答方式化简:$\sqrt{3}$-2$\sqrt{2}$-2|$\sqrt{2}$-$\sqrt{3}$|
分析 先去绝对值符号,再合并同类项即可.
解答 解:原式=$\sqrt{3}$-2$\sqrt{2}$-2$\sqrt{3}$+2$\sqrt{2}$
=(1-2)$\sqrt{3}$+(2-2)$\sqrt{2}$
=-$\sqrt{3}$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
10.在实数0,-π,-4,-$\sqrt{12}$中,最小的数是( )
| A. | 0 | B. | -π | C. | -4 | D. | -$\sqrt{12}$ |
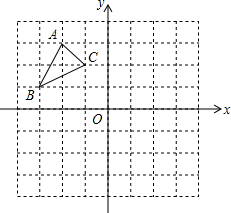 如图,△ABC中A(-2,3),B(-3,1),C(-1,2)
如图,△ABC中A(-2,3),B(-3,1),C(-1,2)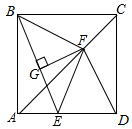 如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:
如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:
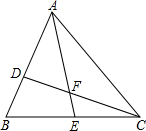 如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.
如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.