题目内容
17．（1）计算：$\frac{b}{a-b}+\frac{a}{a+b}-\frac{2ab}{{{b^2}-{a^2}}}$（2）解方程：$\frac{1}{y-2}+3=\frac{1-y}{2-y}$．
分析 （1）原式通分并利用同分母分式的加减法则计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到y的值，经检验即可得到分式方程的解．
解答 解：（1）原式=$\frac{b（a+b）+a（a-b）+2ab}{（a+b）（a-b）}$=$\frac{（a+b）^{2}}{（a+b）（a-b）}$=$\frac{a+b}{a-b}$；
（2）去分母得：1+3y-6=y-1，
解得：y=2，
经检验y=2是增根，原方程无解．
点评 此题考查了解分式方程，以及分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
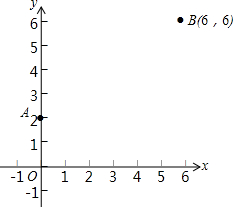如图，已知A（0，2），B（6，6），x轴上一点C到A，B的距离之和为最小，求C点的坐标．
如图，正方形ABCD中，AB=1，点P是BC边上的任意一点（异于端点B、C），连接AP，过B、D两点作BE⊥AP于点E，DF⊥AP于点F．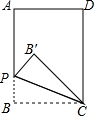
如图，在矩形ABCD中，BC=6，CD=8，点P是AB上（不含端点A，B）任意一点，把△PBC沿PC折叠，当点B的对应点B′落在矩形ABCD对角线上时，BP=3或$\frac{9}{2}$．
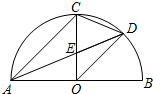如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧BC于点D，AD与OC交于点E，连接CD、OD，给出以下四个结论：
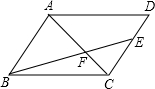如图，在?ABCD中，点E在DC上，EC=2DE，若AC与BE相交于点F，AC=10，则FC=4．