题目内容
12.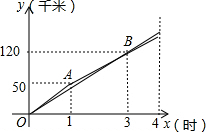 甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练,他们同时同地同向出发,乙在行驶过程中改变了一次速度,甲、乙两人各自在公路上训练时行驶路程y(千米)与行驶时间x(时)(0≤x≤4)之间的函数图象如图所示.
甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练,他们同时同地同向出发,乙在行驶过程中改变了一次速度,甲、乙两人各自在公路上训练时行驶路程y(千米)与行驶时间x(时)(0≤x≤4)之间的函数图象如图所示.(1)求甲行驶的速度.
(2)求直线AB所对应的函数表达式.
(3)直接写出甲、乙相距5千米时x的值.
分析 (1)由速度=路程÷时间,可得出甲行驶的速度;
(2)设直线AB所对应的函数表达式为y=kx+b,将A、B点的坐标代入解析式可得出关于k、b的二元一次方程组,解出方程组即可得出结论;
(3)找出各段线段所对应的函数表达式,根据图象做差可得出关于x的一元一次方程,解方程即可得出结论.
解答 解:(1)120÷3=40(千米/时).
∴甲行驶的速度为40千米/时.
(2)设直线AB所对应的函数表达式为y=kx+b,
把A(1,50)、B(3,120)代入,得
$\left\{\begin{array}{l}{k+b=50}\\{3k+b=120}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=35}\\{b=15}\end{array}\right.$.
故直线AB所对应的函数表达式为y=35x+15(1≤x≤4).
(3)设直线OA所对应的函数表达式为y=k1x,
把A(1,50)代入,得50=k1,
故直线OA所对应的函数表达式为y=50x(0≤x≤1),
设直线OB所对应的函数表达式为y=k2x,
把B(3,120)代入,得120=3k2,
解得:k2=40.
故直线OB所对应的函数表达式为y=40x(0≤x≤4).
当0≤x≤4时,令50x-40x=5,
解得x=0.5;
当1<x≤3时,令35x+15-40x=5,
解得x=2;
当3<x≤4时,令40x-(35x+15)=5,
解得x=4.
综上可知:甲、乙相距5千米时x的值为0.5,2和4.
点评 本题考查了一次函数的应用、待定系数法求函数解析式以及解一元一次方程,解题的关键是:(1)根据速度=路程÷时间求出速度;(2)待定系数法求函数解析式;(3)找出各线段所对应的函数表达式做差即可.本题属于中档题,(1)(2)难度不大,(3)由于要找出各线段的函数解析式,稍显繁琐,在解决该问时一定要细心计算.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
 如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )| A. | 2$\sqrt{6}$ | B. | 5 | C. | 4 | D. | 6 |
 如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为24cm2.
如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为24cm2. 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数. 如图,直线MA∥NB,∠A=68°,∠B=40°,则∠P=28°.
如图,直线MA∥NB,∠A=68°,∠B=40°,则∠P=28°.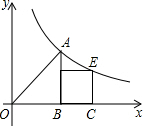 在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.
在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.