题目内容
17．
如图，直线MA∥NB，∠A=68°，∠B=40°，则∠P=28°．
分析 先根据平行线的性质求出∠AOB的度数，再由三角形内角和定理求出∠P的度数．
解答 解：∵直线MA∥NB，∠A=68°，设直线AP与直线NB交于点O，
∴∠A=∠AOB=68°，
又∵∠POB=180°-∠AOB=112°，
∴在三角形POB中，∠B+∠P+∠POB=180°，
∵∠B=40°，
∴∠P=180°-40°-112°=28°．
故答案为：28°．
点评 本题考查的是平行线的性质及三角形外角的性质，先根据题意求出∠POB的度数是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
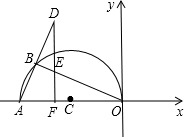在平面直角坐标系中，点A（-5，0），以OA为直径在第二象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，作点A关于点B的对称点D，过点D作x轴垂线，分别交直线OB、x轴于点E、F，点F为垂足，当DF=4时，线段EF=$\frac{3}{2}$或6．
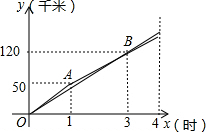甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练，他们同时同地同向出发，乙在行驶过程中改变了一次速度，甲、乙两人各自在公路上训练时行驶路程y（千米）与行驶时间x（时）（0≤x≤4）之间的函数图象如图所示．
甲、乙两车分别从M，N两地沿同一公路相向匀速行驶，两车分别抵达N，M两地后即停止行驶．已知乙车比甲车提前出发，设甲、乙两车之间的路程S（km），乙行驶的时间为t（h），S与t的函数关系如图所示．有下列说法：
9．已知α、β互余，且α比β大30°．则下列方程组中符合题意的是（ ）
| A． | $\left\{\begin{array}{l}α+β=180\\ α=β-30\end{array}\right.$ | B． | $\left\{\begin{array}{l}α+β=180\\ α=β+30\end{array}\right.$ | C． | $\left\{\begin{array}{l}α+β=90\\ α=β+30\end{array}\right.$ | D． | $\left\{\begin{array}{l}α+β=90\\ α=β-30\end{array}\right.$ |
7．若a=b-3，则b-a的值是（ ）
| A． | -3 | B． | 3 | C． | 0 | D． | 6 |