题目内容
8. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=5,∠OBC和∠OCB互余,求DG的长度.
分析 (1)根据三角形的中位线性质求出DG∥BC,EF∥BC,DG=$\frac{1}{2}$BC,EF=$\frac{1}{2}$BC,求出DG∥EF,DG=EF,根据平行四边形的判定得出即可;
(2)求出∠BOC=90°,根据直角三角形的斜边上中线性质得出EF=2OM,即可求出答案.
解答 (1)证明:∵边AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,EF∥BC,DG=$\frac{1}{2}$BC,EF=$\frac{1}{2}$BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90•,
∴∠BOC=90°,
∵M为EF的中点,
∴OM=$\frac{1}{2}$EF,
∵OM=5,DG=EF,
∴DG=EF=2OM=10.
点评 本题考查了三角形的中位线性质,平行四边形的性质,互余,直角三角形斜边上中线性质等知识点,能熟练地运用定理进行推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
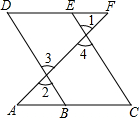 推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由 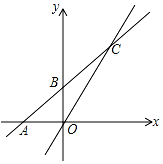 已知一次函数y=kx+b 的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b 的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4) 如图,四边形ABCD和AEFG分别是长方形和正方形,已知正方形的边长是10,△DFG的面积是18.求长方形ABCD的面积.
如图,四边形ABCD和AEFG分别是长方形和正方形,已知正方形的边长是10,△DFG的面积是18.求长方形ABCD的面积.