题目内容
18.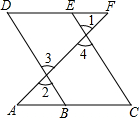 推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由 ∵∠2=∠3,∠1=∠4(对顶角相等 )
又∵∠1=∠2
∴∠3=∠4(等量代换)
∴DB∥CE (内错角相等,两直线平行, )
∴∠C=∠ABD(两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴DF∥AC(同位角相等,两直线平行)
分析 根据对顶角相等得出∠3=∠4,推出DB∥CE,推出∠D=∠ABD,根据平行线判定推出即可.
解答 解:∵∠2=∠3,∠1=∠4(对顶角相等),
又∵∠1=∠2,
∴∠3=∠4(等量代换),
∴DB∥CE(内错角相等,两直线平行),
∴∠C=∠ABD(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换),
∴DF∥AC(同位角相等,两直线平行),
故答案为:对顶角相等,等量代换,DB,CE,内错角相等,两直线平行,两直线平行,同位角相等,已知,等量代换,同位角相等,两直线平行.
点评 此题主要考查了平行线的性质及判定.理清解题思路是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在16≤x<32这个范围的频率为( )
| 棉花纤维长度x | 频数 |
| 0≤x<8 | 1 |
| 8≤x<16 | 2 |
| 16≤x<24 | 8 |
| 24≤x<32 | 6 |
| 32≤x<40 | 3 |
| A. | 0.8 | B. | 0.7 | C. | 0.4 | D. | 0.2 |
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.