题目内容
4.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是45.分析 根据m=2、3、4、5时分裂后首项奇数的规律,得到m3分裂后的首项奇数(用m的式子表示),然后找出分裂后首项奇数最接近2013且小于2013的m,以及分裂后首项奇数最接近2013且大于2013的m,就可解决问题.
解答 解:当m=2时,分裂后的首项奇数为3=2+1=2×1+1;
当m=3时,分裂后的首项奇数为7=6+1=3×2+1;
当m=4时,分裂后的首项奇数为13=12+1=4×3+1;
当m=5时,分裂后的首项奇数为21=20+1=5×4+1;
…
由此可得:m3分裂后的首项奇数为m(m-1)+1;
当m=45时,m(m-1)+1=1981;
当m=46时,m(m-1)+1=2071;
因而当m=45时,m3分裂成的奇数和中有一个奇数是2013.
故答案为45.
点评 本题考查的是数的规律探究,利用熟悉的一列数2、6、12、20…的规律是解决本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
9.已知二次函数y=ax2+bx的图象经过点A(-1,1),则ab有( )
| A. | 最大值1 | B. | 最大值2 | C. | 最小值0 | D. | 最小值$-\frac{1}{4}$ |
 如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD=$\frac{2}{3}$.
如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD=$\frac{2}{3}$.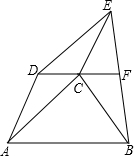 已知:如图,梯形ABCD,AB∥CD,以AC、AD为边向外作?ACED,联结BE,点F是BE的中点,联结CF.求证:CF∥AB.
已知:如图,梯形ABCD,AB∥CD,以AC、AD为边向外作?ACED,联结BE,点F是BE的中点,联结CF.求证:CF∥AB.