题目内容
4. 如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD=$\frac{2}{3}$.
如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD=$\frac{2}{3}$.
分析 作CM⊥AE交AE的延长线于M,作DN⊥AB于N,DF⊥BC于F,AE与BD交于点K,设DK=a,先证明AD:CD=1:2,再证明△BKE≌△CME,得BK=CM=3a,根据tan∠ABD=$\frac{AK}{BK}$即可解决问题.
解答 解:如图,作CM⊥AE交AE的延长线于M,作DN⊥AB于N,DF⊥BC于F,AE与BD交于点K,设DK=a.
∵AB=BE=EC,
∴BC=2AB,
∵DB平分∠ABC,
∴DN=DF,
∵$\frac{{S}_{△ABD}}{{S}_{△BCD}}$=$\frac{\frac{1}{2}•AB•DF}{\frac{1}{2}•CB•DF}$=$\frac{AD}{DC}$,
∴$\frac{AD}{DC}$=$\frac{1}{2}$,$\frac{AD}{AC}$=$\frac{1}{3}$,
∵DB⊥AM,CM⊥AM,
∴DK∥CM,
∴$\frac{DK}{CM}$=$\frac{AD}{AC}$=$\frac{1}{3}$,∠KBE=∠MCE,
∴CM=3a,
在△BKE和△CME中,
$\left\{\begin{array}{l}{∠KBE=∠MCE}\\{∠BEK=∠CEM}\\{BE=EC}\end{array}\right.$,
∴△BKE≌△CME,
∴BK=CM=3a,
∴BD=AE=4a,
∴AK=KE=2a,
∴tan∠ABD=$\frac{AK}{BK}$=$\frac{2a}{3a}$=$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
补充方法:取DC的中点P,连接EP,利用三角形的中位线,可以证明BK=3DK,根据AK=$\frac{1}{2}$BD,
根据tan∠ABD=$\frac{AK}{BK}$=$\frac{2}{3}$.
点评 本题考查翻折变换、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是发现AD:DC=1:2这个条件,学会常用辅助线的添加方法,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)写出y与x的函数关系式;
(2)求出W与x的函数关系式;
(3)售价为150元时,月销售量是多少?
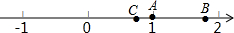 如图所示,数轴上表示1和$\sqrt{3}$对应点分别为A、B,点B到点A的距离等于点C到点O的距离相等,设点C表示的数为x.
如图所示,数轴上表示1和$\sqrt{3}$对应点分别为A、B,点B到点A的距离等于点C到点O的距离相等,设点C表示的数为x.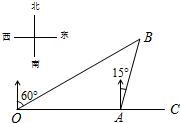 如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.
如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.