题目内容
9．
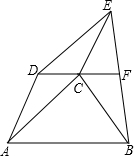已知：如图，梯形ABCD，AB∥CD，以AC、AD为边向外作?ACED，联结BE，点F是BE的中点，联结CF．求证：CF∥AB．
分析 连接AE交DC于点G，易证G是AE的中点，则G是△ABE的中位线，以及过直线外一点有且只有一条直线与已知直线垂直是关键．
解答 
证明：连接AE交DC于点G．
∵四边形ACED是平行四边形，
∴G是AE的中点，
∴连接GF，则GF是△ABE的中位线，
∴GF∥AB，
又∵DC∥AB，
∴直线GF与直线CD重合．
∴CF∥AB．
点评 本题考查了平行线的性质和三角形的中位线定义，正确证明直线CF和直线CD重合是关键．
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
19．若一次函数y=kx+b的图象经过点P（-2，3），则2k-b的值为（ ）
| A． | 2 | B． | -2 | C． | 3 | D． | -3 |
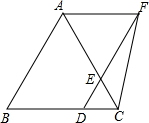已知△ABC为边长为6的等边三角形，D、E分别在边BC、AC上，且CD=CE=x，连接
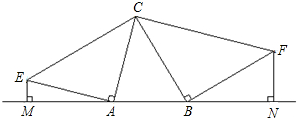如图，锐角△ABC分别以A、B为直角顶点，向△ABC外作等腰直角三角形ACE和等腰直角三角形BCF，再分别过点E、F作边AB所在直线的垂线，垂足为M，N．
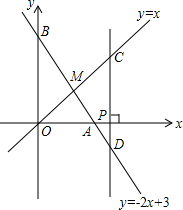如图，已知函数y=-2x+3的图象与x轴、y轴分别交于点A、B，与函数y=x的图象交于点M．在X轴上有一点P（a，0）（其中a＞1），过点P作x轴的垂线，分别交函数y=x和y=-2x+3的图象于点C、D．若CD=3，求a的值．
9．请你估计一下$\frac{（{2}^{2}-1）（{3}^{2}-1）（{4}^{2}-1）…（201{5}^{2}-1）（201{6}^{2}-1）}{{1}^{2}•{2}^{2}•{3}^{2}•{4}^{2}…201{5}^{2}•201{6}^{2}}$的值应该最接近于（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{2016}$ | D． | $\frac{1}{2015}$ |