题目内容
 如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.
如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.考点:解直角三角形
专题:
分析:设AC=k,解Rt△ACB,得出AB=BC=
k,解Rt△ACD,得出AD=
k,然后分别求出这两块三角板的面积,比较即可求解.
| ||
| 2 |
| ||
| 3 |
解答:解:S△ACB<S△ACD.理由如下:
设AC=k.
∵在Rt△ACB中,∠B=90°,∠BAC=∠ACB=45°,
∴AB=BC=
k.
∵在Rt△ACD中,∠CAD=90°,∠D=60°,
∴AD=
=
=
k.
∵S△ACB=
AB•BC=
×
k×
k=
k2,
S△ACD=
AC•AD=
×k×
k=
k2,
又
=
=
,
=
=
,
∴S△ACB<S△ACD.
设AC=k.
∵在Rt△ACB中,∠B=90°,∠BAC=∠ACB=45°,
∴AB=BC=
| ||
| 2 |
∵在Rt△ACD中,∠CAD=90°,∠D=60°,
∴AD=
| AC |
| tanD |
| k | ||
|
| ||
| 3 |
∵S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
又
| 1 |
| 4 |
| 6 |
| 24 |
| ||
| 24 |
| ||
| 6 |
4
| ||
| 24 |
| ||
| 24 |
∴S△ACB<S△ACD.
点评:本题考查了解直角三角形,锐角三角函数的定义,三角形的面积,设AC=k,用含k的代数式表示出AB、BC与AD是解题的关键.

练习册系列答案
相关题目
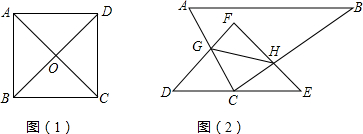
 如图,在一个长方形的空地中央布置一个正方形的花坛,已知正方形的边长比长方形的长短5m,比长方形的宽短1m,且长方形的面积是正方形面积的2倍多5m2,求这个正方形的边长.
如图,在一个长方形的空地中央布置一个正方形的花坛,已知正方形的边长比长方形的长短5m,比长方形的宽短1m,且长方形的面积是正方形面积的2倍多5m2,求这个正方形的边长. 如图,A、B、D在一条直线上,△ABC与△BDE都是等边三角形,F、G、P、Q分别是AC、AD、DE、CE的中点,试判定四边形FGPQ是怎样的特殊四边形?
如图,A、B、D在一条直线上,△ABC与△BDE都是等边三角形,F、G、P、Q分别是AC、AD、DE、CE的中点,试判定四边形FGPQ是怎样的特殊四边形?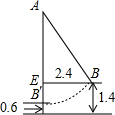 如图是秋千示意图,秋千在平衡位置时,下端B距离地面0.6m,当秋千荡当AB1的位置时,下端B1距离平衡位置的水平距离EB1为2.4m,此时距离地面为1.4m,则秋千AB的长为
如图是秋千示意图,秋千在平衡位置时,下端B距离地面0.6m,当秋千荡当AB1的位置时,下端B1距离平衡位置的水平距离EB1为2.4m,此时距离地面为1.4m,则秋千AB的长为 如图,在锐角△ABC中,BD和CE是两条高,相交于点M,BF和CG是两条角平分线,相交于点N,已知∠BMC=100°,求∠BNC的度数.
如图,在锐角△ABC中,BD和CE是两条高,相交于点M,BF和CG是两条角平分线,相交于点N,已知∠BMC=100°,求∠BNC的度数. 如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.
如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.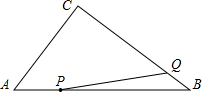 如图,在△ABC中,AB=10cm,BC=8cm,AC=6cm.动点P从点A开始在线段AB上沿A→B→A的路径以每秒2.5cm的速度运动,同时动点Q从点B开始在线段BC上以每秒1cm的速度向点C运动,设点P,Q运动的时间为t秒(0<t<8).
如图,在△ABC中,AB=10cm,BC=8cm,AC=6cm.动点P从点A开始在线段AB上沿A→B→A的路径以每秒2.5cm的速度运动,同时动点Q从点B开始在线段BC上以每秒1cm的速度向点C运动,设点P,Q运动的时间为t秒(0<t<8). 如图,在△ABC的边CA、BA的延长线上分别取点D、E,连接DE,作∠E、∠C的平分线,交于点F.求证:∠F=
如图,在△ABC的边CA、BA的延长线上分别取点D、E,连接DE,作∠E、∠C的平分线,交于点F.求证:∠F=