题目内容
 如图,在一个长方形的空地中央布置一个正方形的花坛,已知正方形的边长比长方形的长短5m,比长方形的宽短1m,且长方形的面积是正方形面积的2倍多5m2,求这个正方形的边长.
如图,在一个长方形的空地中央布置一个正方形的花坛,已知正方形的边长比长方形的长短5m,比长方形的宽短1m,且长方形的面积是正方形面积的2倍多5m2,求这个正方形的边长.考点:一元二次方程的应用
专题:几何图形问题
分析:可设这个正方形的边长是xm,则长方形的长是(x+5)m,长方形的宽是(x+1)m,根据长方形和正方形的面积公式,以及等量关系:长方形的面积是正方形面积的2倍多5m2,列出方程求解即可.
解答:解:设这个正方形的边长是xm,则长方形的长是(x+5)m,长方形的宽是(x+1)m,依题意有
(x+5)(x+1)=2x2+5,
解得x1=6,x2=0(不合题意舍去).
答:这个正方形的边长是6m.
(x+5)(x+1)=2x2+5,
解得x1=6,x2=0(不合题意舍去).
答:这个正方形的边长是6m.
点评:考查了一元二次方程的应用,判断所求的解是否符合题意,舍去不合题意的解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.

练习册系列答案
相关题目
已知∠AOB是平角,过点O作射线OC将∠AOB分成∠AOC和∠BOC,若∠AOC<∠BOC,则∠BOC是( )
| A、锐角 | B、直角 |
| C、钝角 | D、无法确定 |
已知Rt△ABC三个顶点均在函数y=x2上,斜边与x轴平行,则顶点到斜边上高的取值范围为( )
| A、h=1 | B、0<h<1 |
| C、1<h≤2 | D、h>2 |
 如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后送往河岸BC上,再回到P处,请画出旅游船的最短路径.
如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后送往河岸BC上,再回到P处,请画出旅游船的最短路径. 如图,数轴上表示
如图,数轴上表示 如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.
如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.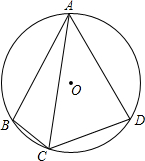 已知:A、B、C、D共圆,AB=AD,∠BAD=60°,AC=a,求S四边形ABCD.
已知:A、B、C、D共圆,AB=AD,∠BAD=60°,AC=a,求S四边形ABCD.