题目内容
 如图,在△ABC的边CA、BA的延长线上分别取点D、E,连接DE,作∠E、∠C的平分线,交于点F.求证:∠F=
如图,在△ABC的边CA、BA的延长线上分别取点D、E,连接DE,作∠E、∠C的平分线,交于点F.求证:∠F=| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:证明题
分析:由CF、EF分别平分∠ACB和∠AED,得∠3=∠4,∠1=∠2,所以有∠3+∠B=∠2+∠F;∠3+∠4+∠B=∠1+∠2+∠D,即2∠3+∠B=2∠2+∠D,而∠B=70°,∠D=40°,于是由两个等式即可求出∠F.
解答:证明:如图,

∵CF、EF分别平分∠ACB和∠AED,
∴∠3=∠4,∠1=∠2,
∵∠3+∠B=∠2+∠F①;
∠3+∠4+∠B=∠1+∠2+∠D,
即2∠3+∠B=2∠2+∠D②,
①×2-②得,
∠B=2∠F-∠D,
∴2∠F=∠B+∠D,
即:∠F=
(∠B+∠D).

∵CF、EF分别平分∠ACB和∠AED,
∴∠3=∠4,∠1=∠2,
∵∠3+∠B=∠2+∠F①;
∠3+∠4+∠B=∠1+∠2+∠D,
即2∠3+∠B=2∠2+∠D②,
①×2-②得,
∠B=2∠F-∠D,
∴2∠F=∠B+∠D,
即:∠F=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.同时考查了角平分线的性质.

练习册系列答案
相关题目
 如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.
如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.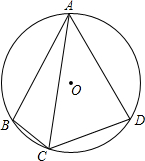 已知:A、B、C、D共圆,AB=AD,∠BAD=60°,AC=a,求S四边形ABCD.
已知:A、B、C、D共圆,AB=AD,∠BAD=60°,AC=a,求S四边形ABCD. 如图所示,由点O引出六条射线OA,OB,OC,OD,OE,OF,且AO⊥OB,OF平分∠BOC,OE平分∠AOD,若∠EOF=170°,求∠COD的度数.
如图所示,由点O引出六条射线OA,OB,OC,OD,OE,OF,且AO⊥OB,OF平分∠BOC,OE平分∠AOD,若∠EOF=170°,求∠COD的度数.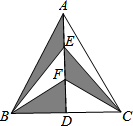 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是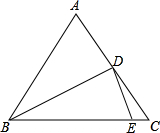 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD交BC于点E,求证:CD=
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD交BC于点E,求证:CD= 如图,直线MN和直线DE分别是线段AB,BC的垂直平分线,它们交于P点,请问PA和PC相等吗?请说明理由.
如图,直线MN和直线DE分别是线段AB,BC的垂直平分线,它们交于P点,请问PA和PC相等吗?请说明理由.