题目内容
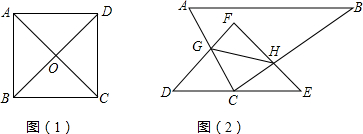
(1)如图(1),正方形ABCD的对角线相交于O点,请问图中有没有等腰直角三角形?若有,请指出是哪几个三角形.
(2)如图(2),在Rt△ABC和Rt△DEF中,∠ACB=∠DFE=90°,DF=EF,C为DE的中点,请问△CGH是等腰直角三角形吗?并说明理由.
(3)在图(2)中,已知点C到EF的距离为4,求四边形CGFH的面积.
(2)如图(2),在Rt△ABC和Rt△DEF中,∠ACB=∠DFE=90°,DF=EF,C为DE的中点,请问△CGH是等腰直角三角形吗?并说明理由.
(3)在图(2)中,已知点C到EF的距离为4,求四边形CGFH的面积.

考点:等腰直角三角形,正方形的性质
专题:
分析:(1)由正方形ABCD的对角线相交于点O,可得等腰直角三角形有:△ABC,△BCD,△ACD,△ABD,△OAB,△OBC,△OCD,△OAD.
(2)根据在等腰直角△DEF中,∠DFE=90°,DF=EF,利用C是DE中点∠D=∠DFC=∠HFC=45°,即可证明:△DCG≌△FCH,得出CG=CH,即可证明△CGH是等腰直角三角形.
(3)根据四边形CGFH的面积=S△FCG+S△FCH=S△FCG+S△DCG=S△DFC=
S△DEF,即可求得四边形CGFH的面积.
(2)根据在等腰直角△DEF中,∠DFE=90°,DF=EF,利用C是DE中点∠D=∠DFC=∠HFC=45°,即可证明:△DCG≌△FCH,得出CG=CH,即可证明△CGH是等腰直角三角形.
(3)根据四边形CGFH的面积=S△FCG+S△FCH=S△FCG+S△DCG=S△DFC=
| 1 |
| 2 |
解答:(1)解:如图(1),∵正方形ABCD的对角线相交于点O,
∴等腰直角三角形有:△ABC,△BCD,△ACD,△ABD,△OAB,△OBC,△OCD,△OAD;

(2)证明:连接CF,在等腰直角△DEF中,∠DFE=90°,DF=EF,
∴∠D=∠E=45°,
又∵C是DE中点,
∴∠DFC=∠EFC=45°,
即∠D=∠DFC=∠HFC=45°,且DC=CF,
∵∠ACB=90°,
∴∠DCG+∠GCF=∠HCF+∠GCF=90°,
∴∠DCG=∠HCF,
在△DCG与△FCH中,
,
∴△DCG≌△FCH(ASA);
∴CG=CH,
∴△CGH是等腰直角三角形.
(3)解:∵△DCG≌△FCH,
∴四边形CGFH的面积=S△FCG+S△FCH=S△FCG+S△DCG=S△DFC=
S△DEF,
∴C到EF的距离为4,C为DE的中点,
∴DF=EF=8,
∴S△DEF=
×8×8=32,
∴四边形CGFH的面积=
S△DEF=
×32=16.
∴等腰直角三角形有:△ABC,△BCD,△ACD,△ABD,△OAB,△OBC,△OCD,△OAD;

(2)证明:连接CF,在等腰直角△DEF中,∠DFE=90°,DF=EF,
∴∠D=∠E=45°,
又∵C是DE中点,
∴∠DFC=∠EFC=45°,
即∠D=∠DFC=∠HFC=45°,且DC=CF,
∵∠ACB=90°,
∴∠DCG+∠GCF=∠HCF+∠GCF=90°,
∴∠DCG=∠HCF,
在△DCG与△FCH中,
|
∴△DCG≌△FCH(ASA);
∴CG=CH,
∴△CGH是等腰直角三角形.
(3)解:∵△DCG≌△FCH,
∴四边形CGFH的面积=S△FCG+S△FCH=S△FCG+S△DCG=S△DFC=
| 1 |
| 2 |
∴C到EF的距离为4,C为DE的中点,
∴DF=EF=8,
∴S△DEF=
| 1 |
| 2 |
∴四边形CGFH的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了正方形的性质,考查了学生对全等三角形的判定与性质和等腰直角三角形的理解和掌握,稍微有点难度,属于中档题.

练习册系列答案
相关题目
已知∠AOB是平角,过点O作射线OC将∠AOB分成∠AOC和∠BOC,若∠AOC<∠BOC,则∠BOC是( )
| A、锐角 | B、直角 |
| C、钝角 | D、无法确定 |
已知Rt△ABC三个顶点均在函数y=x2上,斜边与x轴平行,则顶点到斜边上高的取值范围为( )
| A、h=1 | B、0<h<1 |
| C、1<h≤2 | D、h>2 |
 如图,在△ABC中,D为BC上一点,BD=CD,AD⊥AC于点A,∠BAD=30°.
如图,在△ABC中,D为BC上一点,BD=CD,AD⊥AC于点A,∠BAD=30°. 如图,大圆O1的半径O1A是小圆O2的直径,⊙O1的另一半O1C交⊙O2于B.求证:
如图,大圆O1的半径O1A是小圆O2的直径,⊙O1的另一半O1C交⊙O2于B.求证:
 如图,点E是AB,CD外一点,且AB∥CD,∠BED,∠B,∠D又有何关系,并加以说明.
如图,点E是AB,CD外一点,且AB∥CD,∠BED,∠B,∠D又有何关系,并加以说明. 如图,等边三角形的边长是6,求:
如图,等边三角形的边长是6,求: 如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.
如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.