题目内容
 如图,在锐角△ABC中,BD和CE是两条高,相交于点M,BF和CG是两条角平分线,相交于点N,已知∠BMC=100°,求∠BNC的度数.
如图,在锐角△ABC中,BD和CE是两条高,相交于点M,BF和CG是两条角平分线,相交于点N,已知∠BMC=100°,求∠BNC的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:设∠ECG=x°,∠DBF=y°,根据垂直求出∠BEM=∠CDM=90°,求出∠EBM=∠DCM=10°,根据角平分线定义求出∠ABF=∠CBF=10°-y°,∠ACG=∠BCG=10°+x°,在△EGC中根据三角形内角和定理和三角形外角性质得出∠GEC+∠ECG+∠EGC=180°,∠EGC=∠ABC+∠BCG,代入求出x°-y°=30°,根据三角形内角和定理求出即可.
解答:解:设∠ECG=x°,∠DBF=y°,
∵BD和CE是两条高,
∴∠BEM=∠CDM=90°,
∵∠BMC=100°,
∴∠EBM=∠DCM=100°-90°=10°,
∵BF和CG是两条角平分线,
∴∠ABF=∠CBF=10°-y°,∠ACG=∠BCG=10°+x°,
∵在△EGC中,∠GEC+∠ECG+∠EGC=180°,∠EGC=∠ABC+∠BCG,
∴x°+2(10°-y°)+10°+x°+90°=180°,
∴x°-y°=30°,
∴在△BNC中,∠BNC=180°-(∠NBC+∠NCB)=180°-(10°+x°+10°-y°)
=160°-(x°-y°)
=160°-30°
=130°.
∵BD和CE是两条高,
∴∠BEM=∠CDM=90°,
∵∠BMC=100°,
∴∠EBM=∠DCM=100°-90°=10°,
∵BF和CG是两条角平分线,
∴∠ABF=∠CBF=10°-y°,∠ACG=∠BCG=10°+x°,
∵在△EGC中,∠GEC+∠ECG+∠EGC=180°,∠EGC=∠ABC+∠BCG,
∴x°+2(10°-y°)+10°+x°+90°=180°,
∴x°-y°=30°,
∴在△BNC中,∠BNC=180°-(∠NBC+∠NCB)=180°-(10°+x°+10°-y°)
=160°-(x°-y°)
=160°-30°
=130°.
点评:本题考查了三角形的内角和定理,三角形的外角性质的应用,解此题的关键是求出x°-y°=30°和求出∠BNC=160°-(x°-y°),题目比较好,难度适中.

练习册系列答案
相关题目
 如图,等边三角形的边长是6,求:
如图,等边三角形的边长是6,求: 如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后送往河岸BC上,再回到P处,请画出旅游船的最短路径.
如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后送往河岸BC上,再回到P处,请画出旅游船的最短路径. 如图,大长方形ABCD被分为四个小长方形,其中小长方形AEMF、FMGD、MHCG的面积分别为3、2、4,则△EHD的面积为
如图,大长方形ABCD被分为四个小长方形,其中小长方形AEMF、FMGD、MHCG的面积分别为3、2、4,则△EHD的面积为 如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.
如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由. 如图,BC=2,AC=
如图,BC=2,AC= 如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.
如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD. 如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m.
如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m.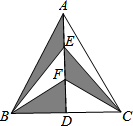 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是