题目内容
 如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.
如图,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.考点:三角形内角和定理,平行线的性质,三角形的外角性质
专题:
分析:由AD平分∠BAC,DE∥AC,且∠EAD=14°,可得:∠BED=28°,然后根据三角形内角和定理即可求出∠BDE的度数,即可判断△BDE的形状.
解答:解:△BDE的形状为直角三角形.
∵AD平分∠BAC,
∴∠BAC=2∠EAD=28°,
∵DE∥AC,
∴∠BED=∠BAC=28°,
∵∠ABC+∠BED+∠BDE=180°,∠ABC=62°,
∴∠BDE=180°-62°-28°=90°,
∴△BDE的形状是直角三角形.
∵AD平分∠BAC,
∴∠BAC=2∠EAD=28°,
∵DE∥AC,
∴∠BED=∠BAC=28°,
∵∠ABC+∠BED+∠BDE=180°,∠ABC=62°,
∴∠BDE=180°-62°-28°=90°,
∴△BDE的形状是直角三角形.
点评:此题考查了三角形内角和定理,角平分线的定义及平行线的性质,解题的关键是:熟记平行线的性质:两直线平行,同位角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知∠AOB是平角,过点O作射线OC将∠AOB分成∠AOC和∠BOC,若∠AOC<∠BOC,则∠BOC是( )
| A、锐角 | B、直角 |
| C、钝角 | D、无法确定 |
张老师和李老师同时从学校出发,骑车去距学校20千米的县城购买书籍,张老师的汽车速度是李老师的1.5倍,结果张老师比李老师早到40分钟.设张老师骑车速度为x千米/小时,依题意,得到的方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
如图,图1,图2,图3分别表示甲乙丙三人由A地到B地的路线图(箭头表示行进的方向),其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( ) 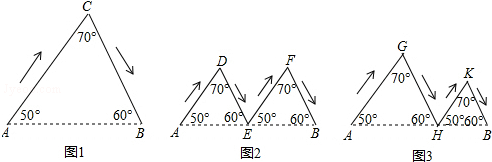

| A、甲<乙<丙 |
| B、甲=乙=丙 |
| C、丙<乙<甲 |
| D、乙<丙<甲 |
 如图,数轴上表示
如图,数轴上表示 如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由.
如图是一副三角板拼成的四边形,含45°角的那一块的斜边恰好等于另一块60°角的对边,试比较这两块三角板面积的大小,并说明理由. 如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.
如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.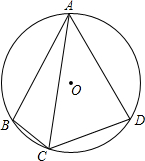 已知:A、B、C、D共圆,AB=AD,∠BAD=60°,AC=a,求S四边形ABCD.
已知:A、B、C、D共圆,AB=AD,∠BAD=60°,AC=a,求S四边形ABCD.