题目内容
9.请你写出一个关于y与x之间的函数关系式y=-x+1,使它满足y随x的增大而减少且函数图象经过点(-1,2).分析 首先可以用待定系数法设此一次函数关系式是:y=kx+b.根据已知条件确定k,b应满足的关系式,再根据条件进行分析即可.
解答 解:设此一次函数关系式是:y=kx+b.
把x=-1,y=2代入得:-k+b=2,即b=2+k;
又根据y随x的增大而减小,知:k<0.
取k=-1,则b=1,此时y=-x+1(答案不唯一).
故答案为y=-x+1.
点评 本题考查了一次函数的性质,掌握待定系数法,首先根据已知条件确定k,b应满足的关系式,再根据条件进行分析即可.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
10.如图,在边长为a的正方形的右下角,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个平行四边形,这一过程可以验证一个关于a,b的等式为( )
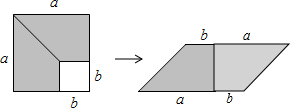

| A. | (a-b)2=a2-2ab+b2 | B. | a2+ab=a(a+b) | C. | (a+b)2=a2+2ab+b2 | D. | a2-b2=(a+b)(a-b) |
11.随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查发现,截至2016年底某市汽车拥有量为16.9万辆,已知2014年底该市汽车拥有量为10万辆,设2014年底至2016年底该市汽车拥有量的年平均增长率为x,根据题意可列方程得( )
| A. | 10(1-x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1+x)2=16.9 | D. | 16.9(1+x)2=10 |
8. 如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )
如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )
 如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )
如图,△ABC∽△BDC,BC=$\sqrt{6}$,AC=3,则CD的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.某物流公司现有31吨货物运往某地,计划同时租用A型车a辆,B型车b辆,使每辆车都装满货物恰好一次运完.
已知每种型号车的载重量和租金如表:
(1)请你帮该物流公司设计租车方案;
(2)请选出最省钱的租车方案,并求出最少租车费.
已知每种型号车的载重量和租金如表:
| 车型 | A | B |
| 载重量(吨/辆) | 3 | 4 |
| 租金(元/辆) | 1000 | 1200 |
(2)请选出最省钱的租车方案,并求出最少租车费.
19.如图1,在边长为4的正△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5.5秒时,PD的长是( )
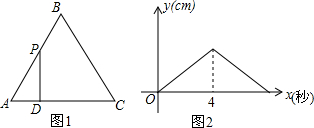

| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
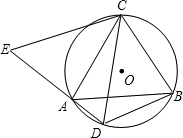 如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.