题目内容
14.某物流公司现有31吨货物运往某地,计划同时租用A型车a辆,B型车b辆,使每辆车都装满货物恰好一次运完.已知每种型号车的载重量和租金如表:
| 车型 | A | B |
| 载重量(吨/辆) | 3 | 4 |
| 租金(元/辆) | 1000 | 1200 |
(2)请选出最省钱的租车方案,并求出最少租车费.
分析 (1)先根据题意得出关于a、b的方程,再根据a、b为正整数即可得出结论;
(2)分别求出各方案的租金,再比较大小即可.
解答 解:(1)∵根据题意得,3a+4b=31,
∴a=$\frac{31-4b}{3}$.
∵a、b为正整数,
∴$\left\{\begin{array}{l}{a=9}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=5}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=1}\\{b=7}\end{array}\right.$,
∴有3种方案:①A型车9辆,B型车1辆;②A型车5辆,B型车4辆;③A型车1辆,B型车7辆.
(2)方案①需租金:9×1000+1200=10200(元);
方案②需租金:5×1000+4×1200=9800(元);
方案③需租金:1×1000+7×1200=9400(元);
∵10200>9800>9400,
∴最省钱的方案是A型车1辆,B型车7辆,最少租车费为9400元.
点评 本题考查的是二元一次方程的应用,根据题意求出a、b的对应值是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.在某校冬季运动会上,有15名选手参加了200米预赛,取前八名进入决赛.已知参赛选手成绩各不相同,某选手要想知道自己是否进入决赛,除了知道自己的成绩外,还需要了解全部成绩的( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
6.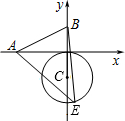 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
 如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )| A. | 2+$\frac{\sqrt{5}}{2}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 3+$\frac{\sqrt{3}}{2}$ | D. | 4+$\frac{\sqrt{3}}{2}$ |
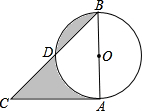 如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图形阴影部分的面积为1.
如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图形阴影部分的面积为1.