题目内容
8．
如图，△ABC∽△BDC，BC=$\sqrt{6}$，AC=3，则CD的长为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据相似三角形的对应边的比相等列式计算即可．
解答 解：∵△ABC∽△BDC，
∴$\frac{BC}{CD}=\frac{AC}{BC}$，
∵BC=$\sqrt{6}$，AC=3，
∴$\frac{\sqrt{6}}{CD}=\frac{3}{\sqrt{6}}$，
解得：CD=2，
故选B．
点评 本题考查了相似三角形的性质，解题的关键是能够根据相似三角形列出正确的比例式并代入数值求解，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
18．
如图，等边三角形ABC内接于⊙O，若AB=3，则图中阴影部分的面积为（ ）
如图，等边三角形ABC内接于⊙O，若AB=3，则图中阴影部分的面积为（ ）| A． | $\frac{3π}{2}-\frac{9}{4}\sqrt{3}$ | B． | $\frac{3π}{2}-\frac{9}{2}\sqrt{3}$ | C． | $π-\frac{3}{4}\sqrt{3}$ | D． | $π-\frac{3}{2}\sqrt{3}$ |
19．下列各式中，计算正确的是（ ）
| A． | （a-4）（a+4）=a2-4 | B． | （4y+1）（4y-1）=16y2-1 | C． | （2x-3）（x+3）=2x2-9 | D． | （x+2）（x+2）=x2+4 |
16．在某校冬季运动会上，有15名选手参加了200米预赛，取前八名进入决赛．已知参赛选手成绩各不相同，某选手要想知道自己是否进入决赛，除了知道自己的成绩外，还需要了解全部成绩的（ ）
| A． | 平均数 | B． | 中位数 | C． | 众数 | D． | 方差 |
3．一个盒子装有除颇色外其它均相同的2个红球和3个白球，现从中任取2个球．则取到的是一个红球、一个白球的概率为（ ）
| A． | 0.2 | B． | 0.3 | C． | 0.4 | D． | 0.6 |
6．
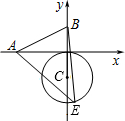如图，已知A、B两点的坐标分别为（-2，0）、（0，1），⊙C的圆心坐标为（0，-1），半径为1，E是⊙C上的一动点，则△ABE面积的最大值为（ ）
如图，已知A、B两点的坐标分别为（-2，0）、（0，1），⊙C的圆心坐标为（0，-1），半径为1，E是⊙C上的一动点，则△ABE面积的最大值为（ ）| A． | 2+$\frac{\sqrt{5}}{2}$ | B． | 3+$\frac{\sqrt{5}}{2}$ | C． | 3+$\frac{\sqrt{3}}{2}$ | D． | 4+$\frac{\sqrt{3}}{2}$ |