题目内容
17.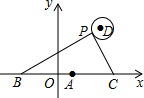 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
分析 首先证明AB=AC=a,根据条件可知PA=AB=AC=a,求出⊙D上到点A的最大距离即可解决问题.
解答 解: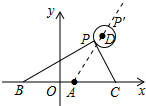 ∵A(1,0),B(1-a,0),C(1+a,0)(a>0),
∵A(1,0),B(1-a,0),C(1+a,0)(a>0),
∴AB=1-(1-a)=a,CA=a+1-1=a,
∴AB=AC,
∵∠BPC=90°,
∴PA=AB=AC=a,
如图延长AD交⊙D于P′,此时AP′最大,
∵A(1,0),D(3,3),
∴AD=$\sqrt{13}$,
∴AP′=$\sqrt{13}$+1,
∴a的最大值为$\sqrt{13}$+1.
故答案为$\sqrt{13}$+1.
点评 本题考查圆、最值问题、直角三角形性质等知识,解题的关键是发现PA=AB=AC=a,求出点P到点A的最大距离即可解决问题,属于中考常考题型.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
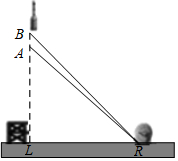 2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AP的距离是6km.仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02).
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AP的距离是6km.仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02).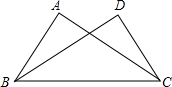 如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是AB=DC.
如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是AB=DC.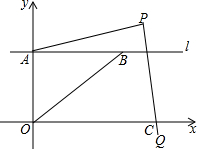 如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,
如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,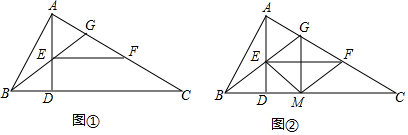
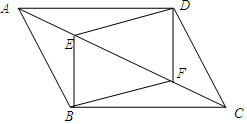 如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC,连结DE、BF.求证:DE=BF.
如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC,连结DE、BF.求证:DE=BF.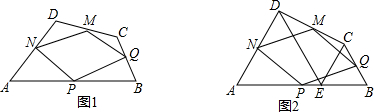
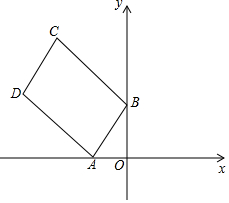 如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上,
如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上, 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),