题目内容
5.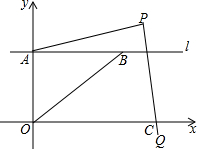 如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,
如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,(1)当动点P与点B重合时,若点B的坐标是(2,1),则PA=2.
(2)当动点P在线段OB的延长线上时,点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,点P到x轴的距离为4,直接写出四边形AOCP的面积.
分析 (1)易得点P的坐标是(2,1),即可得到PA的长.
(2)易证∠AOB=45°,由角平分线的性质可得PM=PN,然后通过证明△ANP≌△CMP即可求出PA:PC的值.
(3)易证四边形OMPN为正方形,进而求出S正方形OMPN,利用三角形全等,进行等积变换,S四边形AOCO=S正方形OMPN.
解答 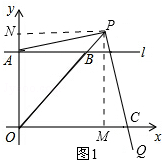 解:(1)∵点P与点B重合,点B的坐标是(2,1),
解:(1)∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
(2)过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示.
∵点A的纵坐标与点B的横坐标相等,
∴OA=AB.
∵∠OAB=90°,
∴∠AOB=∠ABO=45°.
∵∠AOC=90°,
∴∠POC=45°.
∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=∠OMP=90°.
∴∠NPM=90°.
∵∠APC=90°.
∴∠APN=90°-∠APM=∠CPM.
在△ANP和△CMP中,
∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.
∴PA=PC.
∴PA:PC的值为1:1.
(3)∵∠ANP=∠MON=∠OMP=90°
∴四边形OMPN为矩形
∵PM=PN
∴四边形OMPN为正方形
∵点P到x轴的距离为4,
∴PM=PN=4
∴S正方形OMPN=16
∵△ANP≌△CMP.
∴S△ANP=S△CMP.
∴S四边形AOCP=S正方形OMPN=16
点评 此题是三角形综合题,考查了角平分线的性质、全等三角形的判定与性质、矩形和正方形的判定与性质、等腰三角形的判定与性质、勾股定理,等积变换等知识,综合性较强.解(2)的关键时构造全等三角形.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | 3a2•4ab=7a3b | B. | (2ab3)2=4a2b6 | C. | a12÷a6=a2 | D. | 4a+4b=8ab |
5.若x≠0.m是正整数.则下列各式中正确的是( )
| A. | x-m=($\frac{1}{x}$)m | B. | x-m=-xm | C. | x-2m=$\frac{2}{{x}^{m}}$ | D. | (xm)-3=$\frac{m}{{x}^{3}}$ |
 已知,如图,在四边形ABCD中,AD∥BC,点E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.
已知,如图,在四边形ABCD中,AD∥BC,点E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形. 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
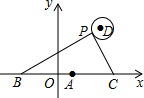 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
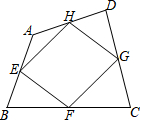 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若四边形EFGH为矩形,则四边形ABCD的对角线AC与BD须满足的关系为AC⊥BD.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若四边形EFGH为矩形,则四边形ABCD的对角线AC与BD须满足的关系为AC⊥BD.