题目内容
9.在四边形ABCD中,AB,BC,CD,DA的中点分别为P,Q,M,N.(1)如图1,试判断四边形PQMN是什么特殊四边形,并证明你的结论.
(2)若在AB边上存在一点E,连接DE,CE,恰好△ADE和△BCE都是等边三角形(图2);
①判断此时四边形PQMN的形状,并证明你的结论;
②当AE=5,BE=4时,求此时四边形PQMN的周长(结果保留根号)
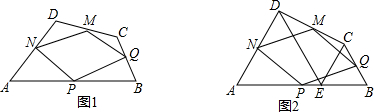
分析 (1)连结AC、BD.利用三角形中位线定理判定四边形PQMN的对边平行且相等,易证该四边形是平行四边形;
(2)先判断出△AEC≌△DEB,得出AC=BD,进而利用中位线得出MN=PN即可得出结论;
(3)先求出DF,BF,进而利用勾股定理求出BD即可得出PN即可得出结论.
解答 解:(1)如图1, 连结AC、BD.
连结AC、BD.
∵AB,BC的中点分别为P,Q,
∴PQ为△ABC的中位线,
∴PQ∥AC,PQ=$\frac{1}{2}$AC,
同理MN∥AC.MN=$\frac{1}{2}$AC.
∴MN=PQ,MN∥PQ,
∴四边形PQMN为平行四边形,
(2)①四边形PQMN是菱形;
如图2,
连接AC,BD,
∵△ADE和△BCE都是等边三角形,
∴AE=DE,CE=BE,∠AED=∠BEC=60°,
∴∠AEC=∠DEB,
∴△AEC≌△DEB,
∴AC=BD,
∵点M,N是AD,CD的中点,
∴MN是△ADC的中位线,
∴MN=$\frac{1}{2}$AC,
同理:PN=$\frac{1}{2}$BD,
∴MN=PN,
由(1)知,四边形MNPQ是平行四边形,
∴平行四边形MNPQ是菱形;
②如图3,
连接BD,过点D作DF⊥AB于F,
∵△ADE是等边三角形,且AE=5,
∴EF=$\frac{1}{2}$AE=$\frac{5}{2}$,
∵DF=$\sqrt{3}$EF=$\frac{5\sqrt{3}}{2}$,
∵BE=4,
∴BF=EF+BE=$\frac{13}{2}$
在Rt△BFD中,根据勾股定理得,BD=$\sqrt{D{F}^{2}+B{F}^{2}}$=$\frac{7\sqrt{5}}{2}$,
由①知,PN=$\frac{1}{2}$BD=$\frac{7\sqrt{5}}{4}$,
由①知,四边形PQMN是菱形,
∴四边形PQMN的周长=4PN=7$\sqrt{5}$.
点评 此题是四边形的综合题,主要考查了三角形的中位线定理,平行四边形的判定,菱形的判定,全等三角形的判定和性质,勾股定理,解(1)的关键是判断出PQ∥AC,PQ=$\frac{1}{2}$AC,解(2)的关键是判断出△AEC≌△DEB,以及构造直角三角形,是一道中等难度的中考常考题.

 阅读快车系列答案
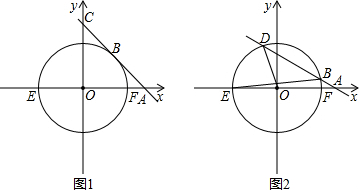
阅读快车系列答案 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.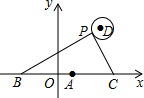 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
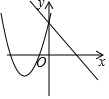
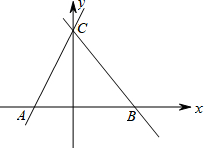 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴的交点分别为B,C,点A的坐标为(-2,0).
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴的交点分别为B,C,点A的坐标为(-2,0).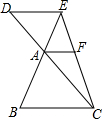 如图,若BC∥DE∥AF 则下列结论中:
如图,若BC∥DE∥AF 则下列结论中: