题目内容
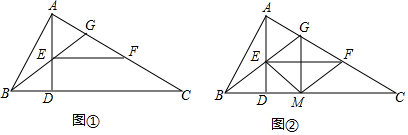
12.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F.(I)求证:AE=CF.
(2)在(1)的基础上,如图②,作GM⊥BC于点M,若GM=GF,连接EM,FM.判断四边形GEMF的形状,并说明理由.
分析 (1)过作E作EH∥AC交CD于H,推出四边形EHCF是平行四边形,根据平行四边形的想折叠的EH=CF,∠C=∠EHB,根据余角的性质得到∠BAD=∠C,根据全等三角形的性质即可得到结论.
(2)根据角平分线的性质得到AG=GM,根据直角三角形的性质得到EG=AG=GF,根据全等三角形的性质得到∠AGB=∠MGB,根据平行线的性质得到∠AEG=∠EGM,推出△AEG是等边三角形,得到∠EAC=∠AGE=60°,于是得到结论.
解答 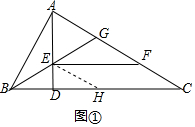 (1)证明:过作E作EH∥AC交CD于H,
(1)证明:过作E作EH∥AC交CD于H,
∵EF∥BC,
∴四边形EHCF是平行四边形,
∴EH=CF,∠C=∠EHB,
∵∠BAC=90°,AD⊥BC于D,
∴∠BAD+∠CAD=∠CAD+∠C=90°,
∴∠BAD=∠C,
∴∠BAD=∠BHE,
∵BG平分∠ABC,
∴∠ABE=∠HBE,
在△ABE与△HBE中,$\left\{\begin{array}{l}{∠ABE=∠HBE}\\{BE=BE}\\{∠BAE=∠BHE}\end{array}\right.$,
∴△ABE≌△HBE,
∴AE=EH,
∴AE=CF;
(2)解:四边形GEMF是菱形,
理由:∵BG平分∠ABC,∠BAC=90°,GM⊥BC,
∴AG=GM,
∵GM=GF,
∴AG=GF,
∵EF∥BC,AD⊥BC,
∴EF⊥AD,
∴∠AEF=90°,
∴EG=AG=GF,
在Rt△ABG与Rt△BMG中,$\left\{\begin{array}{l}{AG=GM}\\{BG=BG}\end{array}\right.$,
∴Rt△ABG≌Rt△BMG,
∴∠AGB=∠MGB,
∵AD∥GM,
∴∠AEG=∠EGM,
∴∠AEG=∠AGE,
∴AE=AG,
∴△AEG是等边三角形,
∴∠EAC=∠AGE=60°,
∴∠BGC=120°,∠C=30°,
∴∠GBC=∠ABE=∠BAE=30°,
∴AE=BE,
∴BE=EG,
∵EF∥BC,
∴GF=CF,
∴EM=EG,MF=GF,
∴EM=EG=MF=GF,
∴四边形GEMF是菱形.
点评 本题考查了全等三角形的判断和性质,角平分线的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的判定和性质,正确的理解题意是解题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.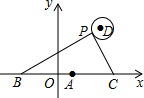 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
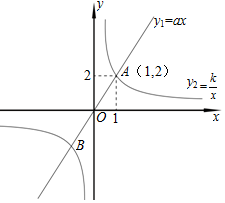 如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).
如图,已知正比例函数y1=ax的图象与反比例函数y2=$\frac{k}{x}$ 的图象有一个公共点A(1,2).