题目内容
19.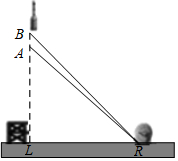 2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AP的距离是6km.仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02).
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AP的距离是6km.仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02).求这枚火箭从A到B的平均速度是多少(结果精确到0.01)?
分析 根据题意直接利用锐角三角函数关系得出LR=AR•cos∠ARL求出答案即可;然后,根据题意直接利用锐角三角函数关系得出BL=LR•tan∠BRL,再利用AL=ARsin∠ARL,求出AB的值,进而得出答案.
解答 解:(1)在Rt△ALR中,AR=6km,∠ARL=42.4°,
由cos∠ARL=$\frac{RL}{AR}$,得LR=AR•cos∠ARL=6×cos42.4°≈4.44(km).
答:发射台与雷达站之间的距离LR为4.44km;
(2)在Rt△BLR中,LR=4.44km,∠BRL=45.5°,
由tan∠BRL=$\frac{BL}{LR}$,得BL=LR•tan∠BRL=4.44×tan45.5°≈4.44×1.02=4.5288(km),
又∵sin∠ARL=$\frac{AL}{AR}$,得AL=ARsin∠ARL=6×sin42.4°≈4.02(km),
∴AB=BL-AL=4.5288-4.02=0.5088≈0.51(km).
答:这枚火箭从A到B的平均速度大约是0.51km/s.
点评 本题主要考查了解直角三角形的应用,正确选择锐角三角函数关系是解题关键.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | 3a2•4ab=7a3b | B. | (2ab3)2=4a2b6 | C. | a12÷a6=a2 | D. | 4a+4b=8ab |
4.下列运算正确的是( )
| A. | 4a•3b=12ab | B. | 4a+3b=7ab | C. | (a-b)2=a2-b2 | D. | (-ab1)2=ab3 |
 已知,如图,在四边形ABCD中,AD∥BC,点E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.
已知,如图,在四边形ABCD中,AD∥BC,点E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.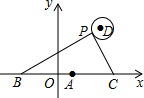 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是$\sqrt{13}+1$.