题目内容
16.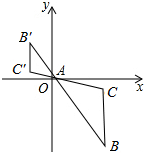 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )| A. | ($\frac{m}{2}$,$\frac{n}{2}$) | B. | (-$\frac{m}{2}$,-$\frac{n}{2}$) | C. | ($\frac{m-3}{2}$,$\frac{n}{2}$) | D. | (-$\frac{m-3}{2}$,-$\frac{n}{2}$) |
分析 过点A作y轴的平行线EF,作GB⊥y轴于G交EF于E,作B′H⊥y轴于H,交EF于F,根据位似变换的性质得到△ABC∽△AB′C′,根据相似三角形的性质计算即可.
解答 解: 过点A作y轴的平行线EF,作GB⊥y轴于G交EF于E,作B′H⊥y轴于H,交EF于F,
过点A作y轴的平行线EF,作GB⊥y轴于G交EF于E,作B′H⊥y轴于H,交EF于F,
由题意得,BE=m-1,AE=-n,
∵△ABC与△AB′C′的位似比为2:1,
∴B′F=$\frac{m-1}{2}$,AF=-$\frac{n}{2}$,
∴B′H=$\frac{m-1}{2}$-1=$\frac{m-3}{2}$,
∴点B′的坐标为(-$\frac{m-3}{2}$,-$\frac{n}{2}$),
故选:D.
点评 本题考查的是位似变换的性质和坐标与图形的性质,掌握两个图形必须是相似形是解题的关键,注意相似三角形的性质的灵活运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11.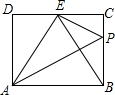 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
 如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )
如图,在矩形ABCD中,点E是CD的中点,AE平分∠BED,PE⊥AE交BC于点P,连接PA,以下四个结论:①BE平分∠AEC;②PA⊥BE;③AD=$\frac{\sqrt{3}}{2}$AB;④PB=2PC.则正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.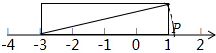 图中长方形的长为4个单位长度、宽为1个单位长度,则点P所表示的数为( )
图中长方形的长为4个单位长度、宽为1个单位长度,则点P所表示的数为( )
 图中长方形的长为4个单位长度、宽为1个单位长度,则点P所表示的数为( )
图中长方形的长为4个单位长度、宽为1个单位长度,则点P所表示的数为( )| A. | $\sqrt{17}-3$ | B. | $\sqrt{17}$ | C. | -$\sqrt{17}+1$ | D. | 无法确定 |
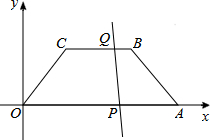 如图,在等腰梯形OABC中BC∥OA,OC=AB,且A(30,0),C(9,14),点P、Q分别是AO边、BC边上的动点,且保持AP=3BQ=2t.
如图,在等腰梯形OABC中BC∥OA,OC=AB,且A(30,0),C(9,14),点P、Q分别是AO边、BC边上的动点,且保持AP=3BQ=2t. 如图,
如图,