题目内容
4.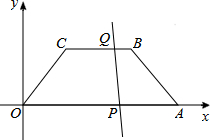 如图,在等腰梯形OABC中BC∥OA,OC=AB,且A(30,0),C(9,14),点P、Q分别是AO边、BC边上的动点,且保持AP=3BQ=2t.
如图,在等腰梯形OABC中BC∥OA,OC=AB,且A(30,0),C(9,14),点P、Q分别是AO边、BC边上的动点,且保持AP=3BQ=2t.(1)求BC的长度;
(2)四边形OPQC能否为平行四边形?若能,求出此时t的值;若不能,说明理由.
(3)若直线PQ将等腰梯形OABC分成面积比为1:2的两个部分,请求出此时的t值.
分析 (1)根据等腰梯形的性质解答即可;
(2)设AP=2t,得出OP=30-2t,利用平行四边形的性质得出CQ=OP,列出关于t的方程解答即可;
(3)根据CQ+OP与QB+AP的比值为1:2或2:1两种情况得出方程解答即可.
解答 解:(1)∵等腰梯形OABC中,A(30,0),C(9,14),
∴BC=30-9-9=12;
(2)设AP=2t,3BQ=2t,
∴OP=30-2t,CQ=12-$\frac{2}{3}t$,
∴当OP=CQ时,四边形OPQC为平行四边形,
可得:30-2t=12-$\frac{2}{3}t$,
解得:t=13.5,
答:当t=13.5时,四边形OPQC为平行四边形;
(3)设AP=2t,3BQ=2t,
∴OP=30-2t,CQ=12-$\frac{2}{3}t$,
当CQ+OP与QB+AP的比值为1:2时,直线PQ将等腰梯形OABC分成面积比为1:2的两个部分,
可得:30-2t+12-$\frac{2}{3}$t=2(2t+$\frac{2}{3}t$),
解得:t=$\frac{21}{4}$,
当CQ+OP与QB+AP的比值为2:1时,直线PQ将等腰梯形OABC分成面积比为1:2的两个部分,
可得:2(30-2t+12-$\frac{2}{3}$t)=2t+$\frac{2}{3}t$,
解得:t=12,
答:当t为$\frac{21}{4}$或12时,直线PQ将等腰梯形OABC分成面积比为1:2的两个部分.
点评 此题考查四边形的综合题,关键是根据等腰梯形的性质和平行四边形的判定解答,注意(3)中CQ+OP与QB+AP的比值为1:2或2:1两种情况解答.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.计算(3a)-1的结果是( )
| A. | $\frac{3}{a}$ | B. | $\frac{1}{3a}$ | C. | 3a | D. | $\frac{a}{3}$ |
16.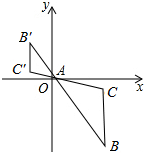 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )| A. | ($\frac{m}{2}$,$\frac{n}{2}$) | B. | (-$\frac{m}{2}$,-$\frac{n}{2}$) | C. | ($\frac{m-3}{2}$,$\frac{n}{2}$) | D. | (-$\frac{m-3}{2}$,-$\frac{n}{2}$) |
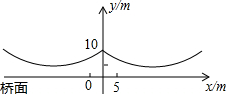 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称. 在数轴上标出下列各数所对应的点A:$\frac{1}{2}$B:$-1\frac{1}{3}$C:2.
在数轴上标出下列各数所对应的点A:$\frac{1}{2}$B:$-1\frac{1}{3}$C:2.