题目内容
8．?ABCD的周长为60，对角线AC、BD交于O，如果△AOB的周长比△BOC的周长大8，则AD=19，CD=11．分析 根据平行四边形的性质可知，平行四边形的对角线互相平分，由于△AOB的周长比△BOC的周长多8，则AB比BC大8，继而可求出AB、BC的长度，由平行四边形的性质即可求出AD，CD的长．
解答 解：∵?ABCD的周长为60，
∴BC+AB=30，①
又∵△AOB的周长比△BOC的周长大8，
∴AB-BC=8，②
由①②得：AB=19，BC=11，
∴CD=19，AD=11，
故答案为：19，11．
点评 此题主要考查平行四边的性质：平行四边形的两组对边分别相等且平行四边形的对角线互相平分．
练习册系列答案
相关题目
16．
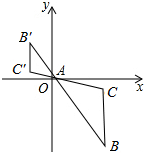如图，△ABC在平面直角坐标系中，A（1，0），B（m，n），以点A为位似中心，在点A的异侧作△ABC位似图形△AB′C′．已知△ABC与△AB′C′的位似比为2：1，则点B′的坐标为（ ）
如图，△ABC在平面直角坐标系中，A（1，0），B（m，n），以点A为位似中心，在点A的异侧作△ABC位似图形△AB′C′．已知△ABC与△AB′C′的位似比为2：1，则点B′的坐标为（ ）| A． | （$\frac{m}{2}$，$\frac{n}{2}$） | B． | （-$\frac{m}{2}$，-$\frac{n}{2}$） | C． | （$\frac{m-3}{2}$，$\frac{n}{2}$） | D． | （-$\frac{m-3}{2}$，-$\frac{n}{2}$） |
3．
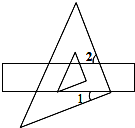如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=25°，则∠2的度数为（ ）
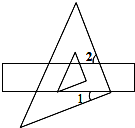如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=25°，则∠2的度数为（ ）| A． | 25° | B． | 65° | C． | 55° | D． | 40° |
在数轴上标出下列各数所对应的点A：$\frac{1}{2}$B：$-1\frac{1}{3}$C：2．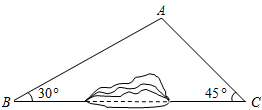
如图所示，因B、C两地之间有一座小山丘阻挡，故无法直接通车．现从B地需经A地才能到达C地．若B、C两地相距6000m，公路AB与BC夹角约为30°，公路AC与BC夹角约为45°，请计算路线B→A→C比BC远了多少米？（参考数据：$\sqrt{3}$≈1.73，$\sqrt{2}$≈1.41，结果保留整数）
17．小明有两根3cm、7cm的木棒，他想以这两根木棒为边做一个三角形，下列不能选用的木棒长为（ ）
| A． | 7cm | B． | 8cm | C． | 9cm | D． | 10cm |
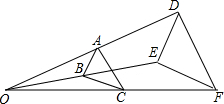如图，△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的$\frac{1}{4}$，则$\frac{AB}{DE}$=$\frac{1}{2}$．