题目内容
8.写出二元一次方程4x-3y=15的一组整数解;一组负整数解;一组正整数解.分析 将x看做已知数求出y,即可确定出一个正整数解,负整数解,整数解.
解答 解:由已知得:y=$\frac{4}{3}$x-5
要使x,y都是整数,
可得一组整数解为$\left\{\begin{array}{l}{x=0}\\{y=-5}\end{array}\right.$;
一组负整数解为$\left\{\begin{array}{l}{x=-3}\\{y=-9}\end{array}\right.$;
一组正整数解为$\left\{\begin{array}{l}{x=6}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.

练习册系列答案
相关题目
17.计算(3a)-1的结果是( )
| A. | $\frac{3}{a}$ | B. | $\frac{1}{3a}$ | C. | 3a | D. | $\frac{a}{3}$ |
16.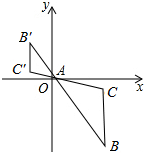 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )| A. | ($\frac{m}{2}$,$\frac{n}{2}$) | B. | (-$\frac{m}{2}$,-$\frac{n}{2}$) | C. | ($\frac{m-3}{2}$,$\frac{n}{2}$) | D. | (-$\frac{m-3}{2}$,-$\frac{n}{2}$) |
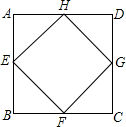 如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.
如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.