题目内容
9.计算:(1)(-3)0-2×23-($\frac{1}{2}$)-2;
(2)(-2a)3-(-a)•(3a)2;
(3)(2x+y)(2x-y)-(2x-y)2;
(4)(a+b-1)(a-b+1)
分析 (1)根据零指数幂与负整数指数幂的意义计算;
(2)先进行积的乘方运算,然后合并同类项即可;
(3)先利用平方差公式和完全平方公式计算,然后合并即可;
(4)先变形得到原式=[a+(b-1)][a-(b-1)],然后利用平方差公式和完全平方公式计算.
解答 解:(1)原式=1-2×8-4
=1-16-4
=-19;
(2)原式=-8a3+a•9a2
=-8a3+9a3
=a3;
(3)原式=4x2-y2-(4x2-4xy+y2)
=4x2-y2-4x2+4xy-y2
=4xy;
(4)原式=[a+(b-1)][a-(b-1)]
=a2-(b-1)2
=a2-(b2-2b+1)
=a2-b2+2b-1.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.计算(3a)-1的结果是( )
| A. | $\frac{3}{a}$ | B. | $\frac{1}{3a}$ | C. | 3a | D. | $\frac{a}{3}$ |
16.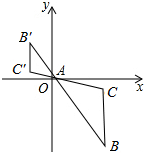 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )| A. | ($\frac{m}{2}$,$\frac{n}{2}$) | B. | (-$\frac{m}{2}$,-$\frac{n}{2}$) | C. | ($\frac{m-3}{2}$,$\frac{n}{2}$) | D. | (-$\frac{m-3}{2}$,-$\frac{n}{2}$) |
17.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,下列不能选用的木棒长为( )
| A. | 7cm | B. | 8cm | C. | 9cm | D. | 10cm |
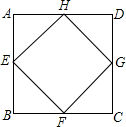 如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.
如图,点E,F,G,H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.