题目内容
5．
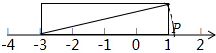图中长方形的长为4个单位长度、宽为1个单位长度，则点P所表示的数为（ ）| A． | $\sqrt{17}-3$ | B． | $\sqrt{17}$ | C． | -$\sqrt{17}+1$ | D． | 无法确定 |
分析 先根据勾股定理求出长方形的对角线的长，再根据同圆的半径相等即可求出点P所表示的数．
解答 解：由勾股定理得，长方形的对角线=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$，
则点P所表示的数为-3+$\sqrt{17}$．
故选A．
点评 本题考查了实数与数轴，勾股定理，本题中正确的计算长方形的对角线的长是解题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17．计算（3a）-1的结果是（ ）
| A． | $\frac{3}{a}$ | B． | $\frac{1}{3a}$ | C． | 3a | D． | $\frac{a}{3}$ |
16．
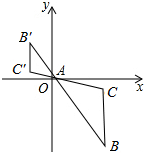如图，△ABC在平面直角坐标系中，A（1，0），B（m，n），以点A为位似中心，在点A的异侧作△ABC位似图形△AB′C′．已知△ABC与△AB′C′的位似比为2：1，则点B′的坐标为（ ）
如图，△ABC在平面直角坐标系中，A（1，0），B（m，n），以点A为位似中心，在点A的异侧作△ABC位似图形△AB′C′．已知△ABC与△AB′C′的位似比为2：1，则点B′的坐标为（ ）| A． | （$\frac{m}{2}$，$\frac{n}{2}$） | B． | （-$\frac{m}{2}$，-$\frac{n}{2}$） | C． | （$\frac{m-3}{2}$，$\frac{n}{2}$） | D． | （-$\frac{m-3}{2}$，-$\frac{n}{2}$） |
在数轴上标出下列各数所对应的点A：$\frac{1}{2}$B：$-1\frac{1}{3}$C：2．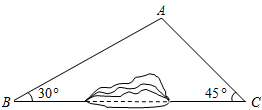
如图所示，因B、C两地之间有一座小山丘阻挡，故无法直接通车．现从B地需经A地才能到达C地．若B、C两地相距6000m，公路AB与BC夹角约为30°，公路AC与BC夹角约为45°，请计算路线B→A→C比BC远了多少米？（参考数据：$\sqrt{3}$≈1.73，$\sqrt{2}$≈1.41，结果保留整数）
17．小明有两根3cm、7cm的木棒，他想以这两根木棒为边做一个三角形，下列不能选用的木棒长为（ ）
| A． | 7cm | B． | 8cm | C． | 9cm | D． | 10cm |