题目内容
1.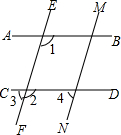 如图,
如图,(1)已知AB∥CD,EF∥MN,∠1=110°,求∠2和∠4的度数;
(2)观察∠1与∠2,∠1与∠4边之间的关系,请你根据(1)的结果进行归纳.试着用文字表述这一规律;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.
分析 (1)根据两直线平行同位角相等、两直线平行同旁内角互补即可解决问题.
(2)通过观察利用(1)的结果可以得到解决.
(3)利用(2)的结论这两个角互补,设未知数列出方程解决.
解答 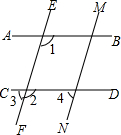 (1)解:∵AB∥CD,
(1)解:∵AB∥CD,
∴∠1=∠2,
∵EF∥MN,
∴∠2+∠4=180°,
∵∠1=110°,
∴∠2=110°,∠4=70°.
(2)观察发现∠1=∠2,∠1+∠=180°,
规律:如果两个角的两边分别平行那么这两个角相等或互补.
(3)设这两个角分别为x,2x.
由结论(2)可知这两个角互补,x+2x=180°,解得x=60°,
所以这两个角分别为60°和120°.
点评 本题考查平行线的性质,两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,学会观察、分析、归纳得出结论并且能应用结论解决问题,属于中考常考题型.

练习册系列答案
相关题目
16.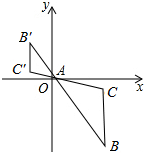 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
 如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )
如图,△ABC在平面直角坐标系中,A(1,0),B(m,n),以点A为位似中心,在点A的异侧作△ABC位似图形△AB′C′.已知△ABC与△AB′C′的位似比为2:1,则点B′的坐标为( )| A. | ($\frac{m}{2}$,$\frac{n}{2}$) | B. | (-$\frac{m}{2}$,-$\frac{n}{2}$) | C. | ($\frac{m-3}{2}$,$\frac{n}{2}$) | D. | (-$\frac{m-3}{2}$,-$\frac{n}{2}$) |
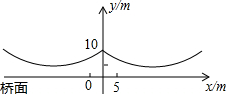 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,右面的一条抛物线可以用y=0.0225x2+0.9x+10 表示,而且左、右两条抛物线关于y轴对称. 在数轴上标出下列各数所对应的点A:$\frac{1}{2}$B:$-1\frac{1}{3}$C:2.
在数轴上标出下列各数所对应的点A:$\frac{1}{2}$B:$-1\frac{1}{3}$C:2.