题目内容
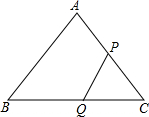 如图,在△ABC中,AB=AC=25cm,BC=30cm,点P从点C出发,沿CA以2.5cm/s的速度向点A运动.同时点Q从B点出发沿BC以4cm/s的速度向C运动,PQ中有一点到达终点时,两点同时停止运动,设运动时间为t.
如图,在△ABC中,AB=AC=25cm,BC=30cm,点P从点C出发,沿CA以2.5cm/s的速度向点A运动.同时点Q从B点出发沿BC以4cm/s的速度向C运动,PQ中有一点到达终点时,两点同时停止运动,设运动时间为t.(1)当CQ=CP时,求t的值;
(2)当t为何值时,PQ∥AB;
(3)设△CPQ的面积为S,求S与t的函数关系式,并直接写出S的取值范围.
考点:平行线分线段成比例,根据实际问题列二次函数关系式,等腰三角形的性质
专题:动点型
分析:(1)利用两点运动路线以及结合运动速度得出CQ=30-4t,CP=2.5t,进而求出即可;
(2)利用平行线的性质得出
=
,进而得出答案;
(3)首先表示出△CPQ的面积为:
×CP×CQsinC,进而得出答案.
(2)利用平行线的性质得出
| CQ |
| CB |
| CP |
| CA |
(3)首先表示出△CPQ的面积为:
| 1 |
| 2 |
解答:解:(1)在△ABC中AB=AC=25cm,BC=30cm,
点P从点C出发,沿CA以2.5cm/秒的速度向点A运动,同时点Q从B点出发沿BC以4cm/秒的速度向点C运动,
PQ中有一点到达终点时,两点同时停止运动,设运动时间为t,
则CQ=30-4t,CP=2.5t,
∵CQ=CP,
∴30-4t=2.5t,
解得:t=
,
即当t=
秒时CQ=CP;
(2)∵PQ∥AB,
∴
=
,
∴
=
,
解得:t=
;
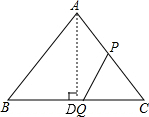
(3)在等腰三角形ABC中,AB=AC=25cm,BC=30cm,
如图所示:设BC边上的高为AD,
则AD=20,sinC=
=
=
,
△CPQ的面积为:
×CP×CQsinC=
(30-4t)×2.5t×
=(30-4t)t,
面积S=-(t-
)2+
,(0<t<7.5),
因为Q点走完BC需要7.5秒,P点走完AC需要10秒,
所以S的取值范围为:0≤S≤
.
点P从点C出发,沿CA以2.5cm/秒的速度向点A运动,同时点Q从B点出发沿BC以4cm/秒的速度向点C运动,
PQ中有一点到达终点时,两点同时停止运动,设运动时间为t,
则CQ=30-4t,CP=2.5t,
∵CQ=CP,
∴30-4t=2.5t,
解得:t=
| 60 |
| 13 |
即当t=
| 60 |
| 13 |
(2)∵PQ∥AB,
∴
| CQ |
| CB |
| CP |
| CA |
∴
| 30-4t |
| 30 |
| 2.5t |
| 25 |

解得:t=
| 30 |
| 7 |
(3)在等腰三角形ABC中,AB=AC=25cm,BC=30cm,
如图所示:设BC边上的高为AD,
则AD=20,sinC=
| AD |
| AC |
| 20 |
| 25 |
| 4 |
| 5 |
△CPQ的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
面积S=-(t-
| 15 |
| 4 |
| 225 |
| 4 |
因为Q点走完BC需要7.5秒,P点走完AC需要10秒,
所以S的取值范围为:0≤S≤
| 225 |
| 4 |
点评:此题主要考查了平行线分线段成比例定理以及锐角三角函数关系和二次函数应用,注意数形结合表示出△CPQ的面积是解题关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,从点O出发的射线有n条,它们依次是OA1,OA2,…,OAn,以这些射线为边的角共有多少个?
如图,从点O出发的射线有n条,它们依次是OA1,OA2,…,OAn,以这些射线为边的角共有多少个?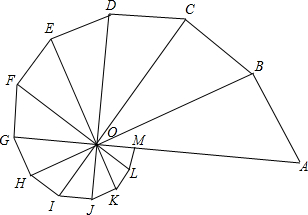 如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?
如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少? 如图,四边形ABCD中,AD∥BC,AC与BD交于点P,点P是BD的黄金分割点(BP大于PD),已知AD=1,求BC的长.
如图,四边形ABCD中,AD∥BC,AC与BD交于点P,点P是BD的黄金分割点(BP大于PD),已知AD=1,求BC的长.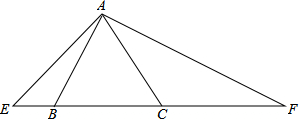 已知∠EAF=120°,它绕着边长为2的正△ABC的顶点A旋转,在正△ABC的左侧,右侧分别交直线BC于E,F.求BE•CF的值.
已知∠EAF=120°,它绕着边长为2的正△ABC的顶点A旋转,在正△ABC的左侧,右侧分别交直线BC于E,F.求BE•CF的值.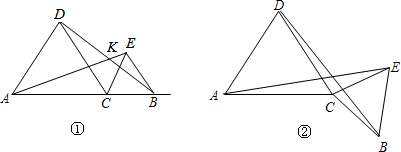
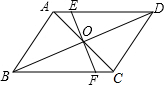 如图,点O为平行四边形ABCD的对角线BD的中点,EF过点O与AD、BC分别相交于点E、F.若B、D两点关于EF对称,请判断四边形EBFD为何种四边形?并说明你的理由.
如图,点O为平行四边形ABCD的对角线BD的中点,EF过点O与AD、BC分别相交于点E、F.若B、D两点关于EF对称,请判断四边形EBFD为何种四边形?并说明你的理由.