题目内容
10.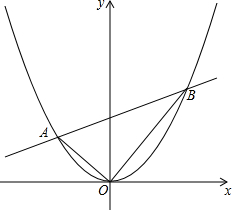 已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)
已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)(1)求A,B两点的横坐标之积和纵坐标之积;
(2)问直线AB是否恒过定点,若是,求出定点坐标,并说明理由.
(3)求△AOB面积的最小值;
(4)若抛物线上有一点C(2,1),将OA⊥OB改为CA⊥CB,直线AB是否恒过定点?若是,直接写出定点坐标,不必说明理由.
分析 (1)设点A的坐标为(x1,y1),点B的坐标为(x2,y2),由两点在抛物线上可得出“${y}_{1}=\frac{1}{4}{{x}_{1}}^{2}$,${y}_{2}=\frac{1}{4}{{x}_{2}}^{2}$”,结合OA⊥OB即两直线斜率乘积为-1可得出$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-1,将y换成x即可得出x1•x2的值,将其代入${y}_{1}•{y}_{2}=\frac{1}{4}{{x}_{1}}^{2}•\frac{1}{4}{{x}_{2}}^{2}$即可得出纵坐标的乘积;
(2)恒过定点(0,4).设直线AB的解析式为y=kx+b,将其代入抛物线y=$\frac{1}{4}$x2中,得出关于x的一元二次方程,由根与系数的关系可求出b值,由此可断定直线AB恒过定点;
(3)利用三角形的面积公式找出S△AOB再根据二次函数的性质即可找出最值问题;
(4)方法类似于(1)(2),不同点在于找到的为(x1+2)(x2+2)=-16,设的直线AB方程为y=k(x+2)+b,求出b值即可得知直线AB恒过点(-2,5).
解答 (1)解:设点A的坐标为(x1,y1),点B的坐标为(x2,y2),
∵A,B是抛物线y=$\frac{1}{4}$x2上的两点,
∴${y}_{1}=\frac{1}{4}{{x}_{1}}^{2}$,${y}_{2}=\frac{1}{4}{{x}_{2}}^{2}$,
∵OA⊥OB,
∴$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-1,即$\frac{1}{4}{x}_{1}•\frac{1}{4}{x}_{2}$=-1,
∴x1•x2=-16,${y}_{1}•{y}_{2}=\frac{1}{4}{{x}_{1}}^{2}•\frac{1}{4}{{x}_{2}}^{2}$=16.
(2)恒过定点(0,4),理由如下:
设直线AB的解析式为y=kx+b.
令$\frac{1}{4}{x}^{2}$=kx+b,即x2-4kx-4b=0,
∴x1+x2=4k,x1•x2=-4b.
又∵x1•x2=-16,即-4b=-16,
∴b=4,
∴直线AB的解析式为y=kx+4,
当x=0时,y=4,
∴直线AB恒过定点(0,4).
(3)S△AOB=$\frac{1}{2}$×4×|x2-x1|=2$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$=2$\sqrt{16{k}^{2}+64}$≥2$\sqrt{64}$=16,
∴当k=0时,△AOB的面积的最小值为16.
(4)直线AB恒过定点(-2,5).理由如下:
设点A的坐标为(x1,y1),点B的坐标为(x2,y2),
∵A,B是抛物线y=$\frac{1}{4}$x2上的两点,
∴${y}_{1}=\frac{1}{4}{{x}_{1}}^{2}$,${y}_{2}=\frac{1}{4}{{x}_{2}}^{2}$,
∵CA⊥CB,
∴$\frac{{y}_{1}-1}{{x}_{1}-2}•\frac{{y}_{2}-1}{{x}_{2}-2}$=-1,即$\frac{1}{4}$(x1+2)•$\frac{1}{4}$(x2+2)=-1,
∴(x1+2)(x2+2)=-16.
设直线AB的解析式为y=k(x+2)+b,
令$\frac{1}{4}$x2=k(x+2)+b,即x2-4k(x+2)-4b=(x+2)2-4(k+1)(x+2)-4b+4=0,
∴(x1+2)+(x2+2)=4(k+1),(x1+2)(x2+2)=-4b+4.
又∵(x1+2)(x2+2)=-16,即-4b+4=-16,
∴b=5,
∴直线AB的解析式为y=k(x+2)+5,
当x=-2时,y=5,
∴直线AB恒过定点(-2,5).
点评 本题考查了根与系数的关系、三角形的面积公式以及二次函数的性质,解题的关键是:(1)根据垂直关系找出$\frac{1}{4}{x}_{1}•\frac{1}{4}{x}_{2}$=-1;(2)根据根与系数的关系找出关于b的一元一次方程;(3)根据二次函数的性质解决最值问题;(4)根据根与系数的关系找出关于b的一元一次方程.本题属于中档题,难度不大,解决该题型题目时,根据根与系数的关系找出关于b的方程是关键.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | cos30° | B. | (-π)0 | C. | -$\frac{1}{3}$ | D. | $\sqrt{64}$ |
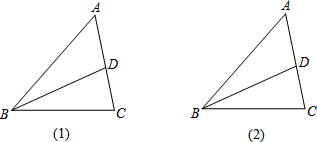
(1)在线段BD上找一点P,使点P到△ABC三条边的距离相等.
(2)在线段BD上找一点Q,使点Q到点B,C的距离相等.
| A. | 互相垂直 | B. | 平行 | ||
| C. | 相交但不垂直 | D. | 平行或相交都有可能 |
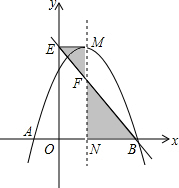 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F. 如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=70°,∠EDF=45°,∠DOB=65°.
如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=70°,∠EDF=45°,∠DOB=65°.