题目内容
11.(1)化简:($\frac{1}{x}$-$\frac{1}{y}$)$÷\frac{{x}^{2}-{y}^{2}}{xy}$(2)解不等式组:$\left\{\begin{array}{l}{3(x-1)≤4x}\\{3-\frac{3}{2}x≥\frac{1}{2}x+1}\end{array}\right.$.
分析 (1)先算括号里面的,再算除法即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=$\frac{-(x-y)}{xy}$•$\frac{xy}{(x+y)(x-y)}$
=-$\frac{1}{x+y}$;
(2)$\left\{\begin{array}{l}3(x-1)≤4x①\\ 3-\frac{3}{2}x≥\frac{1}{2}x+1②\end{array}\right.$,
解不等式①,得x>-3,
解不等式②,得x≤1,
所以原不等式组的解集为-3<x≤1.
点评 本题考查的是分式的混合运算,分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.

练习册系列答案
相关题目
2.若实数a,b满足a2+3a=2,b2+3b=2,且a≠b,则(1+a2)(1+b2)=( )
| A. | 18 | B. | 12 | C. | 9 | D. | 6 |
19.函数y=(m2-m)${x}^{{m}^{2}-3m+1}$是反比例函数,则( )
| A. | m≠0 | B. | m≠0且m≠1 | C. | m=2 | D. | m=1或2 |
 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.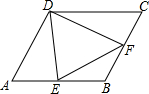 在菱形ABCD中,∠A=60°,E、F分别在AB,BC上,若△DEF有一个角为60°,求证:△DEF一定是等边三角形.
在菱形ABCD中,∠A=60°,E、F分别在AB,BC上,若△DEF有一个角为60°,求证:△DEF一定是等边三角形.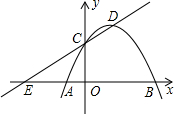 如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$. 如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.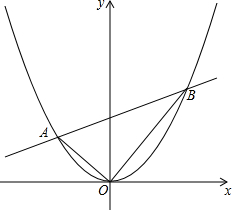 已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)
已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)