题目内容
1.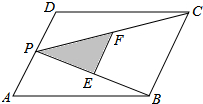 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,若S△PEF=2,则S?ABCD=16.
如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,若S△PEF=2,则S?ABCD=16.
分析 利用三角形中位线定理得出EF∥BC,EF=$\frac{1}{2}$BC,再利用相似三角形的判定与性质得出$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$,进而利用平行四边形的面积求法得出答案.
解答 解:∵E,F分别为PB,PC的中点,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△PEF∽△PBC,
∴$\frac{EF}{BC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$,
∵S△PEF=2,
∴S△PBC=8,
∵四边形ABCD是平行四边形,
∴S?ABCD=2×8=16.
故答案为:16.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质以及三角形中位线定理等知识,得出$\frac{{S}_{△PEF}}{{S}_{△PBC}}$=$\frac{1}{4}$是解题关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
11.下列单项式中,次数为3的是( )
| A. | x3y | B. | x2y | C. | 3xy | D. | 3y |
9.6把钥匙有2把是开大门和房门的(钥匙大小都相同),某人在黑夜摸出钥匙开门,则他一次成功地打开两道门的概率是(打开大门后钥匙不放回)( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
16.在Rt△ABC中,若∠C=90°,cosA=$\frac{3}{5}$,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
6.$\sqrt{(-4)^{2}}$的平方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
10.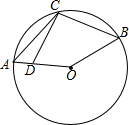 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
 如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )
如图,点C在$\widehat{AB}$上,点D在半径OA上,则下列结论正确的是( )| A. | ∠DCB+$\frac{1}{2}$∠O=180° | B. | ∠ACB+$\frac{1}{2}$∠O=180° | C. | ∠ACB+∠O=180° | D. | ∠CAO+∠CBO=180° |
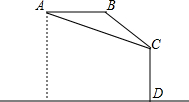 如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.
如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.