题目内容
13.一个三位数,十位、百位上的数字的和等于个位上的数字,十位数字的9倍比个位、百位上的数字的和小2,个位、十位、百位上的数字的和为12,则这个三位数是516.分析 等量关系为:十位上的数字+百位上的数字=个位上的数字;十位上的数字×9=个位数字+百位上的数字-2;个位上的数字+十位上的数字+百位上的数字=12,把相关数值代入可得各位上的数字,三位数=100×百位上的数字+10×十位上的数字+个位数字,把相关数值代入计算可得.
解答 解:这个三位数个位上的数字为x,十位上的数字为y,百位上的数字为z.
$\left\{\begin{array}{l}{y+z=x①}\\{9y=x+z-2②}\\{x+y+z=12③}\end{array}\right.$,
把①代入③得x=6,
把x=6代入①得y+z=6④,
代入②得9y=6+z-2,即9y-z=4⑤
④+⑤得y=1,
则z=5,
则这个三位数为5×100+1×10+6=516.
答:这个三位数是516.
故答案为:516.
点评 考查三元一次方程组的应用.得到各个数位上的数字的等量关系是解决本题的关键;用到的知识点为:三位数=100×百位上的数字+10×十位上的数字+个位数字.

练习册系列答案
相关题目
4.2016年元旦来临之前,为了迎新年,甲、乙两校联合准备文艺汇演,甲、乙两校共92人参加演出(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买演出服装(一人买一套),下面是某服装厂给出的演出服装的价格表:
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有9名准备参加演出的同学抽调去参加科技创新比赛不能参加演出,那么你有几种购买方案,通过比较,你该如何购买服装才能最省钱?
| 购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
| 每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有9名准备参加演出的同学抽调去参加科技创新比赛不能参加演出,那么你有几种购买方案,通过比较,你该如何购买服装才能最省钱?
8. 如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )
如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )
 如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )
如图,在△ABC中,DE∥BC,∠A=60°,∠ADE=50°,则∠C的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
5.关于x的一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的根是( )
| A. | $\frac{b±\sqrt{b^2-4ac}}{2a}$ | B. | $\frac{-b+\sqrt{b^2-4ac}}{2a}$ | C. | $\frac{-b±\sqrt{b^2-4ac}}{2}$ | D. | $\frac{-b±\sqrt{b^2-4ac}}{2a}$ |
2.数轴上与原点距离为5的点表示的是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 6 |
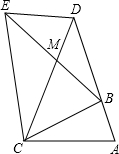 如图,在等腰△ABC中,CB=CA,延长AB至点D,使DB=CB,连接CD,以CD为边作等腰△CDE,使CE=CD,∠ECD=∠BCA,连接BE交CD于点M.
如图,在等腰△ABC中,CB=CA,延长AB至点D,使DB=CB,连接CD,以CD为边作等腰△CDE,使CE=CD,∠ECD=∠BCA,连接BE交CD于点M.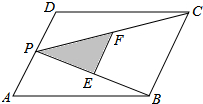 如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,若S△PEF=2,则S?ABCD=16.
如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,若S△PEF=2,则S?ABCD=16.