题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象过点E(2,3),对称轴为x=1,它的图象与x轴交于两点A(x1,0),B(x2,0),且x1<x2,x12+x22=10
(1)求这个二次函数的解析式;
(2)在(1)中抛物线上是否存在点P,使△POA的面积等于△EOB的面积?若存在,求出P点坐标;若不存在,请说明理由.
(1)求这个二次函数的解析式;
(2)在(1)中抛物线上是否存在点P,使△POA的面积等于△EOB的面积?若存在,求出P点坐标;若不存在,请说明理由.
考点:抛物线与x轴的交点
专题:
分析:(1)把E点代入、对称轴表示出来,再结合根与系数的关系可表示出x12+x22=10,可得到关于a、b、c的方程组,求解即可求出二次函数的解析;
(2)可先求得A、B的坐标,求得△EOB的面积,可求得P到OA的距离,代入抛物线可求得P点坐标.
(2)可先求得A、B的坐标,求得△EOB的面积,可求得P到OA的距离,代入抛物线可求得P点坐标.
解答:解:
(1)∵图象过E(2,3),
∴4a+2b+c=3①;
∵对称轴x=1,
∴-
=1②,
∵图象与x轴交于两点A(x1,0),B(x2,0),
∴x1、x2是方程ax2+bx+c=0两根,
∴x1+x2=-
,x1x2=
,
∴x12+x22=(x1+x2)2-2x1x2=
-
=10③,
由①②③可解
,
∴二次函数解析式为y=-x2+2x+3;
(2)在y=-x2+2x+3中,令y=0可得-x2+2x+3=0,解得x=-1或x=3,
∴A为(-1,0)、B为(3,0),
∴OA=1,OB=3,且E为(2,3),
∴S△EOB=
×3×3=
,
设P点坐标为(x,y),则S△POA=
×1×|x|,
∵S△EOB=S△POA,
∴|x|=9,解得x=±9,
当x=9时,代入可得y=-60,
当x=-9时,代入可得y=-96,
∴P点坐标为(9,-60)或(-9,-96),
∴在(1)中抛物线上是存在点P,使△POA的面积等于△EOB的面积,其坐标为(9,-60)或(-9,-96).
(1)∵图象过E(2,3),
∴4a+2b+c=3①;
∵对称轴x=1,
∴-
| b |
| 2a |
∵图象与x轴交于两点A(x1,0),B(x2,0),
∴x1、x2是方程ax2+bx+c=0两根,
∴x1+x2=-
| b |
| a |
| c |
| a |
∴x12+x22=(x1+x2)2-2x1x2=
| b2 |
| a2 |
| 2c |
| a |
由①②③可解
|
∴二次函数解析式为y=-x2+2x+3;
(2)在y=-x2+2x+3中,令y=0可得-x2+2x+3=0,解得x=-1或x=3,
∴A为(-1,0)、B为(3,0),
∴OA=1,OB=3,且E为(2,3),
∴S△EOB=
| 1 |
| 2 |
| 9 |
| 2 |
设P点坐标为(x,y),则S△POA=
| 1 |
| 2 |
∵S△EOB=S△POA,
∴|x|=9,解得x=±9,
当x=9时,代入可得y=-60,
当x=-9时,代入可得y=-96,
∴P点坐标为(9,-60)或(-9,-96),
∴在(1)中抛物线上是存在点P,使△POA的面积等于△EOB的面积,其坐标为(9,-60)或(-9,-96).
点评:本题主要考查待定系数法求函数解析式及二次函数与一元二次方程的关系,在(1)中用a、b、c表示出x12+x22=10是解题的关键,在(2)中求出P点的横坐标是解题的关键.

练习册系列答案
相关题目
若分式
的值为0,则x的值是( )
| 2x-4 |
| x+1 |
| A、2 | ||
| B、-2 | ||
C、
| ||
| D、-1 |
 在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),点A的坐标为(-2,3).
在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),点A的坐标为(-2,3).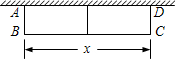 如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.
如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.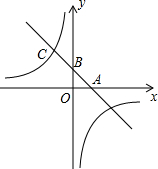 如图,一次函数y=-x+b分别与x轴、y轴交于A、B两点,与反比例函数y=
如图,一次函数y=-x+b分别与x轴、y轴交于A、B两点,与反比例函数y=