题目内容
1.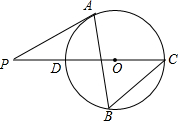 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求证:PA是⊙O的切线;
(2)求证:AC2=CO•CP;
(3)若PD=$\sqrt{3}$,求⊙O的直径.
分析 (1)连结OA、AD,如图,利用圆周角定理得到∠CAD=90°,∠ADC=∠B=60°,则∠ACD=30°,再利用AP=AC得到∠P=∠ACD=30°,接着根据圆周角定理得∠AOD=2∠ACD=60°,然后根据三角形内角和定理可计算出∠OAP=90°,于是根据切线的判定定理可判断AP与⊙O相切;
(2)通过△ACO∽△PCA,得到$\frac{AC}{CP}$=$\frac{OC}{AP}$,由于AC=AP于是得到结论;
(3)连接AD,证得△AOD是等边三角形,得到∠OAD=60°,求得AD=PD=$\sqrt{3}$,得到OD=$\sqrt{3}$,即可得到结论.
解答 (1)证明:连结OA、AD,如图, ∵CD为直径,
∵CD为直径,
∴∠CAD=90°,
∵∠ADC=∠B=60°,
∴∠ACD=30°,
∵AP=AC,
∴∠P=∠ACD=30°,
∵∠AOD=2∠ACD=60°,
∴∠OAP=180°-60°-30°=90°,
∴OA⊥PA,
∴AP与⊙O相切;
(2)证明:∵∠P=∠ACP=∠CAO=30°,
∴△ACO∽△PCA,
∴$\frac{AC}{CP}$=$\frac{OC}{AP}$,
∵AC=AP
∴AC2=CO.CP;
(3)解:连接AD,
∵AO=DO,∠ADC=60°,
∴△AOD是等边三角形,
∴∠OAD=60°,
∴∠PAD=30°,
∴∠P=∠PAD,
∴AD=PD=$\sqrt{3}$,
∴OD=$\sqrt{3}$,
∴⊙O的直径CD=2$\sqrt{3}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质和判定,等边三角形的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
9.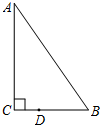 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )| A. | 70° | B. | 70°或120° | C. | 120° | D. | 80° |
13.下列运算中,结果正确的是( )
| A. | 3x2y-2x2y=x2y | B. | 5y-3y=2 | C. | -3x+5x=-8x | D. | 3a+2b=5ab |
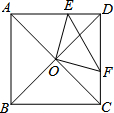 如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.
如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.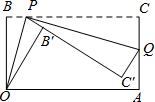 已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为
已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为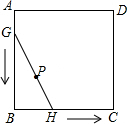 如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π. 已知:如图,PC切⊙O于点C,PA交⊙O于点A,B.
已知:如图,PC切⊙O于点C,PA交⊙O于点A,B. 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.