题目内容
12.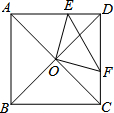 如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.
如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.
分析 由正方形的性质得出∠ADC=90°,∠OAE=∠ODE=∠ODF=∠OCF=45°,OA=OB=OC=OD,AC⊥BD,证出∠AOE=∠DOF,由ASA证明△AOE≌△DOF,得出AE=DF=6,同理:DE=CF=4,由勾股定理求出EF即可.
解答 解:∵四边形ABCD是正方形,
∴∠ADC=90°,∠OAE=∠ODE=∠ODF=∠OCF=45°,OA=OB=OC=OD,AC⊥BD,
∴∠AOD=90°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠AOE=∠DOF,
在△AOE和△DOF中,$\left\{\begin{array}{l}{∠OAE=∠ODF}&{\;}\\{OA=OD}&{\;}\\{∠AOE=∠DOF}&{\;}\end{array}\right.$,
∴△AOE≌△DOF(ASA),
∴AE=DF=6,
同理:DE=CF=4,
∴EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$.
故答案为:2$\sqrt{13}$.
点评 考查了正方形的性质,全等三角形的判定与性质和勾股定理,根据已知条件以及正方形的性质求证出两个全等三角形是解决本题的关键.

练习册系列答案
相关题目
7.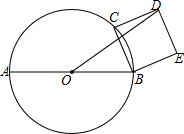 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )| A. | 随点C的运动而变化,最大值为2+2$\sqrt{2}$ | B. | 不变 | ||
| C. | 随点C的运动而变化,最大值为2$\sqrt{2}$ | D. | 随点C的运动而变化,但无最值 |
4.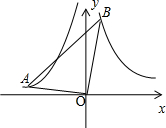 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
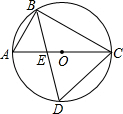 如图.AC是⊙O的直径,点B在⊙O上,∠ACB=30°.作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比.
如图.AC是⊙O的直径,点B在⊙O上,∠ACB=30°.作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比.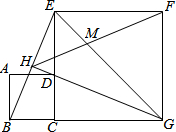 如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.
如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.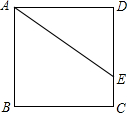 如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为$\sqrt{52}$.
如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为$\sqrt{52}$.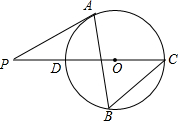 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.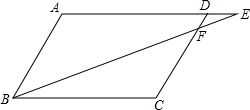 如图,在?ABCD中,E为AD的延长线上的点.求证:
如图,在?ABCD中,E为AD的延长线上的点.求证: