题目内容
12.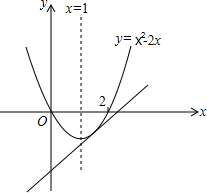 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.(1)求证:无论m取任何实数时,方程总有实数根;
(2)若关于x的二次方程y=mx2-(3m-1)x+2m-2=0的图象经过坐标原点,求抛物线的解析式;
(3)在直角坐标系xOy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
分析 (1)本题中,二次项系数m的值不确定,分为m=0,m≠0两种情况,分别证明方程有实数根.
(2)抛物线经过原点,c=0,列出方程即可解决.
(3)列出方程组,有两个交点,△>0,即可求出b的取值范围.
解答 解:(1)分两种情况讨论.
①当m=0时,方程为x-2=0,x=2.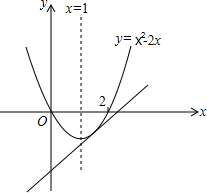
∴m=0时,方程有实数根.
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)
=9m2-6m+1-8m2+8m=m2+2m+1
=(m+1)2≥0,
∴m≠0时,方程有实数根.
故无论m取任何实数时,方程恒有实数根.
综合①②可知,m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根;
(2)∵抛物线y=mx2-(3m-1)x+2m-2经过原点,
∴2m-2=0,
∴m=1,
∴抛物线解析式为y=x2-2x.
(3)函数图象如图所示,由$\left\{\begin{array}{l}{y={x}^{2}-2x}\\{y=x+b}\end{array}\right.$消去y得到x2-3x-b=0,
∵两个函数图象有两个交点,
∴△>O,
∴9+4b>0,
∴b>-$\frac{9}{4}$时直线y=x+b与(2)中的函数图象只有两个交点.
点评 本题考查了一元二次方程的根的情况,二次函数与对应的一元二次方程的联系,讨论一次函数与二次函数图象交点的情况,记住两个函数图象有两个交点,说明方程组有两组解,利用判别式解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
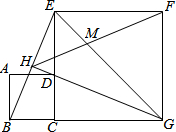 如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.
如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.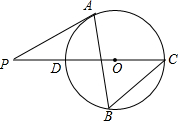 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.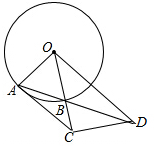 已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.
已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$. 如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).
如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).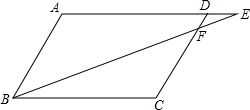 如图,在?ABCD中,E为AD的延长线上的点.求证:
如图,在?ABCD中,E为AD的延长线上的点.求证: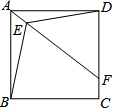 如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.
如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.