题目内容
16.(1)计算:$\sqrt{12}-{(-\frac{1}{2})^{-2}}+{(1-\sqrt{3})^0}-4sin{60°}$(2)先化简,再求值:$\frac{{{a^2}-1}}{{{a^2}-a}}÷(2+\frac{{{a^2}+1}}{a})$,其中$a=\sqrt{2}-1$.
分析 (1)根据负整数指数幂、零指数幂的定义、二次根式的运算法则化简即可.
(2)先计算括号,然后计算除法,后代入计算解决.
解答 解:(1)原式=2$\sqrt{3}$-4+1-2$\sqrt{3}$=-3
(2)原式=$\frac{(a+1)(a-1)}{a(a-1)}$÷$\frac{{a}^{2}+2a+1}{a}$=$\frac{a+1}{a}$•$\frac{a}{(a+1)^{2}}$=$\frac{1}{a+1}$,
当a=$\sqrt{2}$-1时,原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查分式的化简求值、实数的运算、零指数幂、负整数指数幂的定义、特殊角的三角函数值等整数,解题的关键是熟练掌握这些法则以及定义,属于中考常考题型.

练习册系列答案
相关题目
1.二次根式$\sqrt{a-b}$的有理化因式是( )
| A. | $\sqrt{a+b}$ | B. | $\sqrt{a}$+$\sqrt{b}$ | C. | $\sqrt{a-b}$ | D. | $\sqrt{a}$-$\sqrt{b}$ |
5.若$\sqrt{{(a-4)}^{2}}$=a-4,则a的取值范围是( )
| A. | a<4 | B. | a≤4 | C. | a>4 | D. | a≥4 |
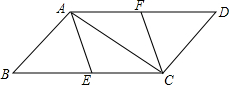 如图,?ABCD中,E,F分别为BC,AD的中点.
如图,?ABCD中,E,F分别为BC,AD的中点.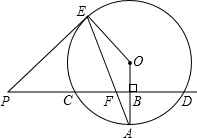 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.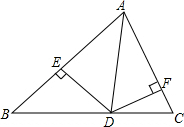 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论:
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论: 如图,直线AB:y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,直线上一动点P以1cm/s的速度由点A向终点B运动,设运动时间为t(s).
如图,直线AB:y=-$\frac{\sqrt{6}}{2}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,直线上一动点P以1cm/s的速度由点A向终点B运动,设运动时间为t(s).