题目内容
11.计算(1)-t3•(-t)4÷(-t)5
(2)(-1)2015+2-1-($\frac{3}{2}$)-2+(π-3.14)0
(3)(a-b)2•(a-b)n•(b-a)3
(4 ) 2(x3)2•x3-(4x3)3+(-3x)4•x5.
分析 (1)根据同底数幂的乘除法法则计算即可求解;
(2)先算乘方、负整数指数幂和零指数幂,再算加减法即可求解;
(3)根据同底数幂的乘法法则计算即可求解;
(4)先算幂的乘方和积的乘方、再算同底数幂的乘法,再合并同类项即可求解.
解答 解:(1)-t3•(-t)4÷(-t)5
=t3+4-5
=t2;
(2)(-1)2015+2-1-($\frac{3}{2}$)-2+(π-3.14)0
=-1+$\frac{1}{2}$-$\frac{4}{9}$+1
=$\frac{1}{18}$;
(3)(a-b)2•(a-b)n•(b-a)3
=-(a-b)2+n+3
=-(a-b)5+n;
(4 ) 2(x3)2•x3-(4x3)3+(-3x)4•x5.
=2x6•x3-64x9+81x4•x5
=2x9-64x9+81x9
=19x9.
点评 本题主要考查整式的混合运算,同底数幂的乘法,积的乘方,合并同类项,负整数指数幂、绝对值、零指数幂和乘方的运用,熟记公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.计算$\sqrt{(-2-{x}^{2})^{2}}$的结果是( )
| A. | -2-x2 | B. | 2+x2 | C. | -2+x2 | D. | 2-x2 |
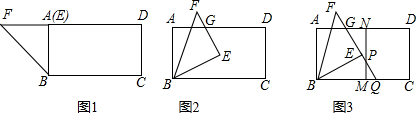
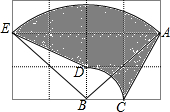 如图所示,格点△ABC绕点B逆时针旋转得到△EBD,图中每个小正方形的边长是1,则图中阴影部分的面积为$\frac{7π}{4}$.
如图所示,格点△ABC绕点B逆时针旋转得到△EBD,图中每个小正方形的边长是1,则图中阴影部分的面积为$\frac{7π}{4}$.