题目内容
8.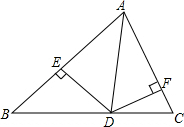 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论:
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论:(1)△ADE≌△ADF;(2)△BDE≌△CDF;(3)△ABD≌△ACD;(4)AE=AF;(5)BE=CF;(6)BD=CD;(7)∠ADE=∠ADF
正确的有①④⑦(只填序号)
分析 由角平分线易得DE=DF,根据HL证明△ADE≌△ADF,利用全等三角形的性质判断即可.
解答 解:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵DE是△ABD的高,DF是△ACD的高,
∴DE=DF,
在△ADE与△ADF中,$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADF(HL),
∴AE=AF,∠ADE=∠ADF,
故正确是①④⑦,
故答案为:①④⑦.
点评 本题考查了全等三角形的判定和性质,角平分线的性质.做题时要注意思路:由已知结合性质与图形进行思考,由易到难,步步深入.

练习册系列答案
相关题目
19.计算$\sqrt{(-2-{x}^{2})^{2}}$的结果是( )
| A. | -2-x2 | B. | 2+x2 | C. | -2+x2 | D. | 2-x2 |
17.下列命题中,是真命题的是( )
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 依次连接四边形四边中点所组成的图形是矩形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
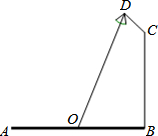 如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.
如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳.此时,路灯的灯柱BC高度应该设计为(11$\sqrt{3}$-4)米.