题目内容
4.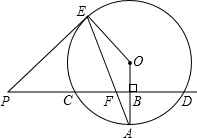 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.(1)证明:PE=PF;
(2)若PF=26,sinA=$\frac{5}{13}$,求EF的长.
分析 (1)由PE是⊙O的切线,易证得∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF;
(2)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PF•sinA=26×$\frac{5}{13}$=10,又由等腰三角形的性质,求得答案.
解答 解:(1)∵PE是⊙O的切线,
∴∠PEO=90°,
∴∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,
∵OE=OA,
∴∠A=∠AEO,
∴∠PEF=∠PFE,
∴PE=PF;
(2)过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°,
∵∠PFG=∠AFB,
∴∠FPG=∠A,
∴FG=PF•sinA=26×$\frac{5}{13}$=10,
∵PE=PF,
∴EF=2FG=20.
点评 此题考查了切线的性质、等腰三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
11.下表列出了一项试验统计数据,表示将皮球从高处落下时,下落高度d与弹跳高度b的关系:
(1)下落高度d与弹跳高度b之间的函数解析式是C
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
15.我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
| A. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$ |
19.计算$\sqrt{(-2-{x}^{2})^{2}}$的结果是( )
| A. | -2-x2 | B. | 2+x2 | C. | -2+x2 | D. | 2-x2 |
14.下列剪纸图案中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |