题目内容
7.(1)($\sqrt{3}$+$\sqrt{6}$)2(2)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$
(3)$\sqrt{18}+{(\sqrt{2}+1)^{-1}}+{(-2)^{-2}}$
(4)$\frac{2}{3}\sqrt{3\frac{3}{4}}×(-9\sqrt{45})$.
分析 (1)根据完全平方公式将原式展开,然后再合并同类项即可解答本题;
(2)先将原式化简再合并同类项即可解答本题;
(3)先将原式化简再合并同类项即可解答本题;
(4)先将原式化简在相乘约分即可.
解答 解:(1)($\sqrt{3}$+$\sqrt{6}$)2
=$(\sqrt{3})^{2}+2\sqrt{3}×\sqrt{6}+(\sqrt{6})^{2}$
=3+$6\sqrt{2}$+6
=9+$6\sqrt{2}$;
(2)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$
=$4\sqrt{5}+3\sqrt{5}-2\sqrt{2}+4\sqrt{2}$
=$7\sqrt{5}+2\sqrt{2}$;
(3)$\sqrt{18}+{(\sqrt{2}+1)^{-1}}+{(-2)^{-2}}$
=$3\sqrt{2}+\frac{1}{\sqrt{2}+1}+\frac{1}{4}$
=$3\sqrt{2}+\sqrt{2}-1+\frac{1}{4}$
=$4\sqrt{2}-\frac{3}{4}$;
(4)$\frac{2}{3}\sqrt{3\frac{3}{4}}×(-9\sqrt{45})$
=$\frac{2}{3}×\sqrt{\frac{15}{4}}×(-27\sqrt{5})$
=-$\frac{2}{3}×\frac{\sqrt{15}}{2}×27\sqrt{5}$
=-45$\sqrt{3}$.
点评 本题考查二次根式的混合运算、负整数指数幂,解题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
相关题目
15.我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
| A. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$ |
19.计算$\sqrt{(-2-{x}^{2})^{2}}$的结果是( )
| A. | -2-x2 | B. | 2+x2 | C. | -2+x2 | D. | 2-x2 |
17.下列命题中,是真命题的是( )
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 依次连接四边形四边中点所组成的图形是矩形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
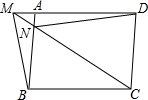 如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.
如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.