题目内容
3.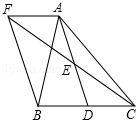 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;
(2)①当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
②当△ABC满足什么条件时,四边形AFBD是菱形?并说明理由.
分析 (1)由△AEF≌△DEC得出AF=DC,再根据已知条件即可证明.
(2)①当AB=AC时,四边形AFBD是矩形.先证明四边形AFBD是平行四边形,再证明∠ADB=90°即可.
②当∠BAC=90°时,四边形AFBD是菱形.先证明四边形AFBD是平行四边形,再证明AD=BD即可.
解答 (1)证明:∵E是AD的中点,
∴AE=ED,
∵AF∥BC,
∴∠AFE=∠ECD,
在△AEF和△DEC中,
$\left\{\begin{array}{l}{∠AFE=∠ECD}\\{∠AEF=∠DEC}\\{AE=ED}\end{array}\right.$,
∴△AEF≌△DEC,
∴AF=DC,
∵AF=BD,
∴BD=DC.
(2)①当AB=AC时,四边形AFBD是矩形.
证明:∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AFBD是矩形.
②当∠BAC=90°时,四边形AFBD是菱形.
证明::∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形,
∵∠BAC=90°,BD=DC,
∴AD=BD=DC,
∴四边形AFBD是菱形.
点评 本题考查菱形的判定、矩形的判定、等腰三角形的性质、直角三角形斜边中线定理等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目

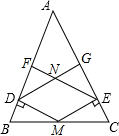 已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.
已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.