题目内容
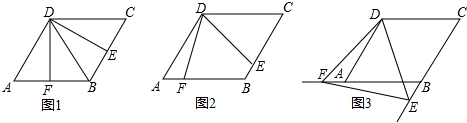
13.如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)在(2)的条件下连EF,若△DEF的面积为y,BE=x,求y与x的关系式.
分析 (1)由菱形的性质得到△ABD是等边三角形,再证明△ADF≌△BDE即可;
(2)由菱形的性质得到△ABD是等边三角形,再证明△ADF≌△BDE即可;
(3)利用全等三角形的面积相等,再直接计算面积.
解答 (1)DF=DE.
证明:如图2,连接BD,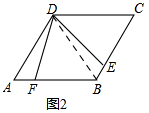
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE,
在△ADF与△BDE中,
$\left\{\begin{array}{l}{∠ADF=∠BDE}\\{AD=BD}\\{∠A=∠DBE}\end{array}\right.$,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)DF=DE.
如图3,连接BD.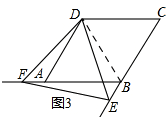
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
在△ADF与△BDE中,
$\left\{\begin{array}{l}{∠ADF=∠BDE}\\{AD=BD}\\{∠DAF=∠DBE}\end{array}\right.$,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)由(2)知,△ADF≌△BDE.则S△ADF=S△BDE,
设AF=BE=x.
∴y=S△BEF+S△ABD=$\frac{1}{2}$(2+x)$\frac{{\sqrt{3}}}{2}$x+$\frac{1}{2}$×2×2×$\frac{{\sqrt{3}}}{2}$=$\frac{\sqrt{3}}{4}$(x+1)2+$\frac{3\sqrt{3}}{4}$.
即y=$\frac{\sqrt{3}}{4}$(x+1)2+$\frac{3\sqrt{3}}{4}$.
点评 此题几何变换综合题,主要考查了菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,判断三角形是等边三角形(△ABD是等边三角形)是解本题的关键.


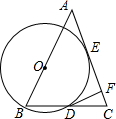 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1. 已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.
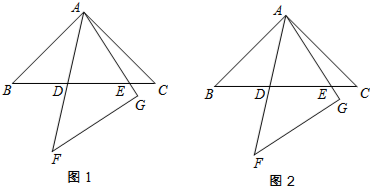
已知实数a,b在数轴上对应点的位置如图所示,化简b-$\sqrt{(a-b)^{2}}$=a.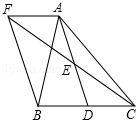 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.